PROGRAM ASPECTS

Chapter 10. Fluid volumes: the computer simulation program FLUIDS

The figures - as referenced in the text - are not ready yet. See the textbook itself. (R. Min, Academic Book Center, De Lier, 1995)

This chapter discusses:

a case studies about the body fluid volumes and electrolytes as well as respiratory control mechanisms;
Which parameters can be used for a learning and training environment?
Which variables are important for insight or training in this field?
What are the most important educational aspects of this simulation programs?

Introduction

This chapter describes the computer simulation program FLUIDS. The mathematical model underlying this program contains over 200 variables and describes control mechanisms of body fluid volumes and electrolytes as well as respiratory control mechanisms. This model allows a variety of simulations of e.g. thirst, fluid loss, exaggerated drinking, carbon dioxide inhalation, severe physical exercise, etc. The student can again infuse fluids of different compositions, give a diuretic, etc. The basic physiology of respiratory and metabolic acidosis and alkalosis can be studied with this model.

Aim of instruction

The computer simulation program FLUIDS enables students to experiment with a model of the human water and electrolyte system and the regulation of respiration and its underlying (basic) physiology and pathophysiology. The simulation consists of the following: heart and cardiovascular system, lungs, intra- and extra cellular fluid compartments, nerve reflections, the kidney, and a number of hormonal systems with an influence on the kidney function. In some ways this simulation coincides with the model of the computer simulation program CARDIO, but in several important parts it is much more extensive. The computer simulation program FLUIDS simulates a kind of experimental laboratory environment, so that students can do research on water and salt regulation and the regulation of respiration under various circumstances.

Figure 10.1. A screendump of the computer simulation program FLUIDS designed with MacTHESIS.

Students have 'a testee' at their disposal so to speak, with which they can do a series of experiments. Thus it is possible, for example, to imitate excessive thirsting, sweating, or excessive loss of water and salt. A change in the oxygen and carbon dioxide fraction during breathing can also be simulated. Furthermore disorders in the acid-base balance can be simulated and the function of the kidney .
Beside interventions with the potential of making the patient ill, therapeutic interventions are also possible, such as applying infusions of various compositions in order to give extra oxygen for breathing or the administration of a diuretic. It is also possible to do the so-called glucose tolerance test (GTT). Despite the complexity of the model it has been observed that students can easily find their way in this computer simulation program. In this simulation the emphasis is on free investigation in order to develop in the students an overall picture of the way the human body works as a complex physiological dynamic system.

Model of the water and electrolyte regulation

The model of the computer simulation program FLUIDS is a model of the water and electrolyte regulation of a healthy male of 55 kg. The model of the regulation of the body fluids was designed by Ikeda, Marumo, Shiritako, and Sato in 1979 and is based on a.o. Guyton (1972) and Blaine (1972). (Ikeda et al., 1979).

The model by Ikeda and co-workers consists of the following sub-systems: circulation, respiration, kidney function, and the intra- and extra-cellular fluid compartments. In all the model consists of 30 integral equations plus other algebraic equations, totalling more than 270 variables. Water and salt regulation varies greatly among individuals and also between the sexes. In this model (a young man of 55 kg) the body fluids are divided into three major groups: the intracellular (20.0 liter), the interstitial (8.8 liter) and the intravascular compartment (2.2 liter). The relatively small amount of transcellular water (brain fluid, fluid in the stomach and intestinal canal, eye compartment fluid and such) is not taken into account and only plays a small role in the total weight. The extracellular volume is 11.0 liter and the blood volume 4.0 liter. The composition of blood plasma, interstitial fluid and extracellular fluid, as well as that of the dissolved ionized matter and the molecular dissolved matter of gasses, is very specific.
The normal values of ion concentrations and others in the extracellular and intracellular fluid compartments in the computer simulation program FLUIDS are:

	Extracellular concentrations:	Intracellular concentrations:
Sodium Na⁺	140 mEq/l	10 mEq/l
Chlorine Cl^-	104 mEq/l	4 mEq/l
Potassium K⁺	4.5 mEq/l	140 mEq/l
Calcium Ca⁺⁺	5 mEq/l	<< 0.001 mEq/l
Magnesium Mg⁺⁺	3 mEq/l	58 mEq/l
Bicarbonate HCO3^-	24 mEq/l	10 mEq/l
Phosphate PO4^---	1.1 mEq/l	75 mEq/l
Sulphate SO4^--	1 mEq/l	2 mEq/l
Glucose	6 mosmol/l	0 mosmol/l
Urea	2.5 mosmol/l	2.5 mosmol/l

There are many regulation mechanisms to keep changes in the concentrations in the extra- and intra-cellular fluid compartments as small as possible. The kidney plays an important part here, by regulating the volume and the colloid osmotic pressure of the fluid compartments. In addition there are regulation mechanisms for the degree of acid, for the stabilization of the blood gas pressure of O2 and CO2, for the stabilization of the ionic composition, and for the stabilization of the glucose percentage. The model includes seven parts that can be distinguished, and the relations between them are shown in Figure 10.2. This figure also indicates some interventions which are possible in this model. The different parts of the model as shown in Figure 10.2 are:

Cardiovascular system
The cardiovascular system has been minimized to a functional unit for the cardiac output and the mean arterial pressure, which in this model depend only on the blood volume, elasticity of the vascular system, and the peripheral resistance. Because the cardiovascular system has been so minimized, simulation of a cardiovascular affliction is not easy with this model.

Respiratory system
The regulating system of respiration is a functional unit in which ventilation depends on the pH, the CO2-, and the O2-pressure in the arterial blood. The pH of the blood is determined by the percentage of freely dissolved CO2 and the percentage of HCO3-. The equation of Henderson-Hassalbalch is valid here. The hemoglobin buffer system can keep the pH of the blood constant by the intake or release of H+-ions, although there are situations when a large or fast increase or decrease of H+-ions takes place.

(See the

book)
Figure 10.2. Block outline of the model by Ikeda et al. (1979) of the water and electrolyte regulation. The arrows going into the blocks, are the possibilities of interventions, the arrows touching the edges of the blocks are input variables and the arrows leaving the blocks are output variables.

(See the

book)
Figure 10.3. Thirsting, sweating and loss of salt (QIWL = 0.008 l/min, YNIN = -1.2 mEq/min and YCLI = -1.2 mEq/min). The intake of water is 0 l/min (QIN = 0.0) (Min, 1982).

The pH in the blood is largely determined by animo acids, composed of proteins. This buffer system of H+-ions regulates the pH around 7.4 (iso-hydric point). Another buffer system for the pH is the bicarbonate buffer. The proper functioning of this system requires the CO2 surplus to be adequately removed via the lungs.

Extracellular fluid compartment
This part of the model simulates the regulation of the fluid volumes. The dissolved ion concentration in the extra-cellular fluid compartment is closely connected to the quantity of water taken in and excreted by the body. The fluid volume in the extra-cellular compartment is determined by the quantity of water which is administered orally or intravenously and by the loss of fluid in the form of urine and sweat. The intake of concentrations of the dissolved matter held in this system usually comes via food from the stomach and intestines. Intravenous administration through an infuse is also possible in this model. All intakes have been normalized on an average of 24 hours with certain referential values per minute.

Intracellular fluid compartment and electrolytes
In this part of the model Ikeda and co-workers have classified the intracellular fluid volume, the osmotic active substances in the intra- and extra-cellular compartments and the intra-cellular acid-base balance, among others sodium, potassium, chlorine, glucose, ureum and mannitol. The change in the extra cellular sodium quantity (ZNE) is represented in the model as follows:

d(ZNE)/dt = intake by Na(YNIN) - excretion of Na(YNU) + increase of Na, in exchange for H⁺-ions in the cell

and the change of the quantity of potassium in the extra-cellular compartment (ZKE) like this:

d(ZKE)/dt = intake of K(YKIN) - excretion of K(YKU) + increase of K, in exchange for H⁺-ions in the cell - K which goes into the cell in connection with glucose metabolism and insulin secretion.

The ureum reabsorption mechanism in this model is passive while it is assumed that about 60% of the filtered quantity will eventually be excreted. The plasma osmolality (OSMP) depends in this model on the sodium, potassium, chlorine, glucose, ureum and mannitol concentrations, and on a constant factor for the other osmotic active substances.

The kidney
The renal excretion for bicarbonate, calcium, magnesium, phosphate, and organic acids are in this model functions of the glomerular filtration velocity and the concentrations of these ions. A quantity of fluid from the plasma is filtered through the glomerulus. The blood pressure is the driving force in this model. The largest part of the filtrate returns then, selectively, into the plasma in the peritubular capillaries.

The transport of potassium and sodium is active, going against the concentration gradient as well as the electric gradient. The negative ions, like chlorine, diffuse passively, with the exception of bicarbonate. The transport of water only happens if there is an osmotic driving power. The model attempts to keep the osmolality of the plasma constant. Chemoreceptors play an important part here. The active transport of ions and the transport of water is influenced by hormones. In this model the active transport of sodium is aided by aldosterone which retains (reabsorbs) sodium and excretes potassium. The excretion of water can be checked by the antidiuretic hormone.

(See the

book)
Figure 10.4. A simulation experiment with the computer simulation program FLUIDS, during 3 hours (180 minutes) at which an infusion is given of Physiological salt of 1 litre with 154 mEq sodium and chlorine during 5 minutes (QVIN = 0.2 l/min, YNIN = 31 and YCLI is 31 mEq/min during 5 minutes) (Min, 1982).

Construction of the model
Below the formulation of the most essential parts of the various blocks is described.

The circulation
The cardiac output (QCO) is only dependent on the blood volume (BV) and determines together with the total peripheral resistance (RTOT) the mean arterial pressure (PAS).

The fluid volumes
The plasma volume (VP) is determined by the quantity of water which is administered intravenously (QVIN), the quantity which is taken in by the body orally (QIN), the quantity of water which leaves the body in the form of urine (QWU) and also by a.o. the quantity of water which leaves the body through sweating (QIWL) and that which is formed metabolically (QMWP).
The blood volume (VB) and the extracellular fluid volume (VEC) are ultimately determined by the plasma volume. The interstitial fluid volume (VIF) is calculated in a similar way.

The Na, K and Cl concentrations
The sodium concentration in the extracellular fluid (XNE) depends on the quantity of water in the extracellular compartment (VEC) and the absolute quantity of sodium (ZNE). The absolute quantity of sodium is, among others, a function of the mean average daily sodium intake (YNIN) and the quantity which leaves the body in the form of urine (YNU). The same holds true for potassium (XKE, ZKE, YKIN, YKU) and chlorine (XCLE, ZCLE, YCLI, YCLU) . The model is similarly built for calcium, magnesium, glucose, bicarbonate, phosphate, sulphate, urea, mannitol, other organic acids, and proteins.

Kidney and urine
The osmolality of urine (OSMU) is determined by the urine output (QWU), the glomerular filtration velocity (GFR) and the antidiuretic hormone (ADH).
The pH of the urine (PHU) is calculated a.o. from the renal clarification velocity of organic salts (YORG) and phosphate (YPO4).

The glomerular filtration velocity
The glomerular filtration velocity (GFR) is only a function of the mean arterial pressure (PAS) and the extra-cellular fluid volume (VEC) here.

Respiration
The ventilation (VI) is determined by a function (F) of the CO2 pressure (PCOA), the O2 pressure in the alveoli (PO2A) and the pH of the arterial blood (PHA). The pH in the alveoli (PHA) is calculated with the Henderson-Hasselbalch equation.

Results

The computer simulation program FLUIDS, built with the RLCS system of the University of Limburg, measures and registers in its starting position eight important variables.

These values are only valid when no interventions have taken place in the model and one can speak of a steady state. In the casuistry here described in respect of thirsting, sweating, drinking, and infuses other variables often play an important role. Therefore it is also possible to measure and register other arbitrary variables. If some of these variables exceed or fall below a critical value, the students will be warned by a message.
The symptoms appearing in the computer simulation program FLUIDS are determined by a range of values. As soon as they come above or below a certain level, a message is given to the student:

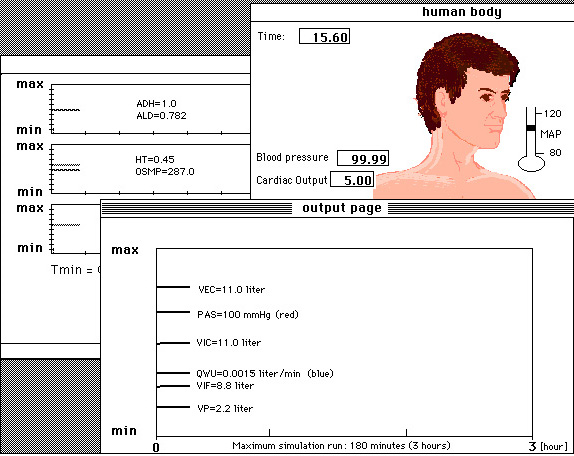
Figure 10.5. A screendump of the computer simulation program FLUIDS designed with MacTHESIS.

Thirsting, sweating and loss of salt
An important simulation is to withhold water from the testee (the model) over an extended period. When there is also loss of fluid (QIWI) and much loss of salt (via YNIN and YCLI) together with the thirsting, as can be seen in Figure 10.3. During the simulation time the water intake is QIN = 0 l/min and the velocity with which fluid is withdrawn (QWIL) from the body has increased from 0.007 l/min to 0.008 l/min (which is equal to 0.5 l/hour). The sodium and chlorine intake (YNIN and YCLI), which are normally 0.12 respectively 0.133 mEq/min, are both fixed on -1.2 mEq/min. It can clearly be seen that the ADH increases and the urine excretion reduces sharply. The blood pressure (PAS) falls, in contrast with the situation of drinking pure water only in which the osmolality of plasma and urine increases slightly.

Water intake: drinking, water-infuse or physiological salt infuse
Water intake can be simulated by the model in three ways: drinking, hypertonic infuse or a physiological salt infuse.
Figures 10.4 shows the consequences of intravenous injection of one litre of physiological salt in five minutes, while the sodium (YNIN) and intake are both 31 mEq/min. This is equal to a quantity of sodium and chlorine of 154 mEq. The figure shows how the model reacts with a rise in blood pressure (PAS). Here also the kidney will act as a regulator: due to the rise in blood pressure the kidney will excrete salt. This lasts for several hours. When the salt is being excreted the water excretion will follow.

Discussion

The computer simulation program FLUIDS was used for the first time in 1981/1982 at the University of Limburg at Maastricht in the curriculum block 'The adult'. A condition for presentation in education a complex model as used in FLUIDS is that one has the disposal of a series of good work sheets. One of the educational goals in this block is the study of the water and salt regulation and the case which is developed by co-workers and student assistants is based on a case of this block. Aspects from this case, such as thirsting, sweating, drinking (sea)water, and giving the desiccated person a physiological salt infuse, are all discussed. Many students have done these experiments and they showed in their subsequent discussions the willingness to tackle more problems in the teaching group and to study them more closely in literature.
Working with the computer simulation program FLUIDS and the complex model of the water and electrolyte regulation requires from the teacher a good preparation of the casual relationships involved in the model and the student needs a good case in a workbook or on worksheets to be used as a guide. The results with this model are illuminating for the student and give good cause for further study of the water and electrolyte regulation.
As mentioned in the chapter on the computer simulation program CARDIO in 1987, the computer simulation programs FLUIDS and CARDIO (both implemented in the RLCS-system), have now had about 3000 student sessions at the University of Limburg. The model is implemented in the MacTHESIS system in 1990 (see figure 10.5). It is also implemented in THESIS system for MS.DOS computers.

References

Min, F.B.M., (1996)
Simulation Technology & Parallelism in Learning Environments; Methods, Concepts, Models and Systems. Publisher: Academic Book Center, De Lier. ISBN 90-5478-036-3

Min, F.B.M., (1993)
Biomedical Modelling and simulation on a PC; A Workbench for Physiology and Biomedical Engineering (3 chapters). Springer-Verlag New York Berlin; (Editors: R. van Wijk van Brievingh and D. M�ller).

Note
The first version of this chapter was first published in Dutch in: Min 1982; Ph.D thesis, University of Limburg, Maastricht and in English in: D. Möller and R. Van Wijk van Brievingh (editors), Springer Verlag, Berlin.

Note
The complete model listing in Fortran is given by R. Van Wijk van Brievingh and D. Möller (1993). In this book an executable MS.DOS version on floppy of FLUIDS has been enclosed. There is also nowe a listing in Pascal. We are working also for a source writen in Java now.

Note about the figures:
See them all of better quality in the real existing book: Rik Min, Simulation Technology & Parallelism in Learning Environments; Methods, Concepts, Models and Systems. Publisher: Academic Book Center, De Lier. Holland. ISBN 90-5478-036-3 (1996).

Acknowledgement
The author gratefully acknowledges the contribution of Dr. Ikeda and his co-workers at Kitasato University, Japan, to the computer simulation program FLUIDS.