MULTIMEDIALE LEERMIDDELEN --- HOOFDSTUK

Een algemeen dynamisch denk-model voor leren: een analogon

Door R. Min, P.Kommers, H. Vos (allen Universiteit Twente) en C. van Dijkum (Universiteit Utrecht) (nog in bewerking; nog in discussie in kleine kring; nog niet elders gepubliceerd) (updated: 15 mei 1998)

Key-words: leren, leer-model, instructie, studeerbaarheid, motivatie, vergeten, instructiebronnen, instructiemiddelen, leermiddelen, feedback systemen, modellen, modelvorming, een 'model voor leren' versus een 'leer-model'.

Samenvatting

Inleiding

Binnen de onderwijskunde wordt traditioneel weinig onderzoek gedaan naar het opstellen van deterministische modellen die verschijnselen kunnen vastleggen en nabootsen zoals die zich voordoen bij het leren of instrueren met name conceptuele modellen in de vorm van wiskundige vergelijkingen of analogons zie je weinig. Er wordt wel redelijk veel onderzoek gedaan naar relaties tussen ontwerpvariabelen en leereffecten bij bijvoorbeeld docent-leerling instructiesituaties of computer-based leren. Maar het is niet altijd helemaal na te gaan met welk en hoeveel succes. Laat staan dat onderzoekers hun bevindingen aangaande leer-effecten in mathematische modellen publiceren.

We willen uitspraken onderzoeken en relaties vastleggen zoals: 'hoe kun je door motivatie de weerstand tegen leren laten afnemen? In ons onderzoek is gebleken dat de motivatie voor het volgen van een 'saaie' lessen toeneemt als er in het curriculum goede leermiddelen zijn opgenomen. Als er een zoals dat heet 'gedifferentieerd leermiddelen aanbod' is - en de leermidddelen zelf zijn ook motiverend - dan motiveert dat een leerling om saaiere lessen (of saaie boeken) over dat onderwerp (goed) te volgen. Maar ook vragen als: welke vormen van instructie en welke vormen van feedback bij simulatie zijn het meest geschikt om de motivatie voor leren bij de leerling te bevorderen? Of vragen meer van deze tijd: hoe kun je door goede leermiddelen de studeerbaarheid van de lessen verhogen? Of anders: hoe kun je door de studeerbaarheid te verhogen de weerstanden bij leerprocessen laten afnemen?

Definitie: (Model-driven) simulatie is (hier) een open interactieve leeromgeving - gebaseerd op een model van een werkelijkheid - waarbij in laatste instantie dat onderliggende wiskundig model bepaalt hoe het op een aktie van een gebruiker (hier: een lerende) reageert.

Definitie: Intelligente Computer Simulatie (ICS) is model-driven simulatie met een rule base welke elke simulatiestap (dt) het dynamisch gedrag van het model 'monitor-t' en - naast de gewone feedback - een bepaald soort (extra) feedback aan de gebruiker geeft. (Zie figuur 4.)

Definitie: Een model van leren is een (vooralsnog kwalitatief) een-een-duidig vastgelegd model (of analogon) van fenomenen (meestal kennisvermeerdering) zoals die voorkomen bij het gebruik van leer- of instructiemiddelen.

Atkinson poneerde in 1977 een model in de vorm van een differentiaal vergelijking. Men noemde dat de 'leervergelijking'; men sprak van de kennistoename in Atkinson's 'leervergelijking'. De theoretische basis daarvan lag in het 'broadcast process', waarbij gekeken werd hoe een bericht via media wordt overgedragen en hoe berichten diffunderen in een populatie van N personen. De parameter a kan in dit geval opgevat worden als het percentage van de totale populatie dat iedere keer geconverteerd wordt als het (zelfde) bericht wordt uitgezonden.

Als we kijken hoe kennisverwerving of leren verloopt, dan is er - onder invloed van instructie of lezen van een tekst - een curve te veronderstellen zoals in figuur 1 schematisch is aangegeven. Al jaren lang bestaat er het 'leer-model' van Atkinsson. Dat leer-model geeft een modelmatige, deterministische beschrijving. Dit model geeft als het ware een beschrijving aangaande de 'leer- of kennistoename'. Een diepere ontleding van dat model komt uit op een differentiaal vergelijking van het type dq/dt = a (I-q), waarbij I de input (stimulus) is, bijvoorbeeld een instructie en de output q de actuele kennis en met name het nivo daarvan; dq/dt is de toename van q in de tijd. De 'toename' is in deze vergelijking gelijk aan een constant percentage van hetgeen nog resteert, d.w.z. wat iemand nog moet leren (I-q). De analoge oplossing voor dergelijke vergelijkingen laten we in dit artikel buiten beschouwing. We willen een simulatiestudie doen (op een PC) en derhalve is de diffentiaalvergelijking representatiewijze an sich voldoende.

Figuur 1. Hoe verloopt het leerproces? Hoe snel neemt men iets op? Hoe snel leert men? Is opnemen hetzelfde als leren? Welke parameters zijn daarvoor verantwoordelijk? De doelen ('normen' of 'goals') die men zich stelt? Een leerling stelt zich een doel; als het doel bereikt is stopt hij/zij met leren; het niveau aan kennis, vaardigheden of inzichten wat hij/zij zich had gesteld, is bereikt. Hoe verloopt het vergeten? etc. Hier is te zien dat leren kennis accumulatie is en dat vergeten het omgekeerde is.

Dit model komt ook voor bij de 'diffusievergelijking' van het 'broadcast proces' (Vos en Min, collegediktaat, 1997/98) en de toename van de lading en de spanning in een condensator: du/dt = 1/RC (E-u). Ook het feedbackmodel van Lava en March (1975) en Spada en Kempf (1977) hebben die structuur. Kommers (1991) beschrijft in zijn proefschrift ook iets dergelijks: het model van Anderson 'the architecture of cognition'. In dat model komt de vergelijking da/dt = n - p*a voor. In het discrete geval is dat een differentie vergelijking. Al deze modellen kenmerken zich door een eerste orde differentiaal vergelijking waarbij de toename van de gemodelleerde variabele (d.../dt) wordt bepaald door een stimulus (een inputvariabele, bijvoorbeeld: I, E of n), door de eigenschappen van een persoon zelf (een parameter) en door de actuele waarde van de variabele. Bij het model van Atkinson wordt die parameter 'intelligentie' genoemd (a of 1/RC). Als we kijken naar al deze modellen dan zijn ze feitelijk analoog aan elkaar. Dit artikel wil deze analogie aanhouden en een nieuw model voorstellen. In dat nieuwe model zitten ook de parameters: motivatie, studeerbaarheid, vergeten en het zelf kunnen kiezen uit een gedifferentieerd leermiddelen- en instructiemiddelen-aanbod (de stimuli). Zie ook de (stochastische) modellen van Bush en Mosteller (1995).

Figuur 2a. A wil iets vertellen aan B; of B wil iets horen van A, maar de vraag is: loopt een en ander goed en onthoudt B alles?

Figuur 2b. Kennis A wordt door een leerling B opgenomen, maar wanneer gaat dat vlot en wanneer gaat dat slecht? en waarmee gaat dat het beste?

De eersten werken vanuit een idee van 'aanbod' van instructiemiddelen. De tweede soort van uit een idee van 'vraag' naar instructie of iets dergelijks. Het is opvallend hoe weinig men weet van de leereffecten die deze media bij de leerling bewerkstelligen. Men weet binnen de (traditionele) onderwijskunde veel over instructie maar weinig over het opnemen, verwerken van kennis en het verkrijgen van inzicht, d.w.z.: van het echte actieve leren en de daarbij horende leerprocessen, weerstanden en hoe motivationele ontwerpvariabelen daarop inspelen.

Figuur 3a. Studeerbaarheid zowel als motivatie kun je zien als een 'weerstand' tegen het 'opnemen van kennis'.

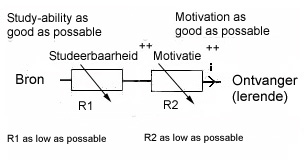
Figuur 3b. Als de motivatie voor het aangebodenen laag is, kun je zeggen dat de 'weerstand tegen het aangebodene' dus hoog is; omgekeerd als de studeerbaarheid goed is is de 'weerstand tegen het aangebodenen' dus laag. Deze weerstanden staan dus in serie tussen de bron (A) en degene die moeten leren (B).

Instructiemiddelen zijn meestal wel goed doordacht, maar over open leeromgevingen - en hoe het leren en het geheugen nu precies werkt - is weinig bekend. Een van de dingen die onderzoekers in hun onderlinge contacten ontberen is een goed en valide model van leren en het bijbehorende leerproces. We weten dat goede leermiddelen als het ware de 'weerstand tegen het leren' verminderd. Dat willen we in deze aanpak eens letterlijk nemen. In dit artikel willen wij ingaan op oude ideeen over 'vergeten' en 'onthouden' en nieuwe ideeen over hoe je de 'weerstand tegen saaie lessen' weg kunt nemen door goede leermiddelen te gebruiken - bijvoorbeeld multimediale computersimulaties of games - die paden banen die andere middelen niet kunnen bewerkstelligen. In het kader van de discussies over een 'zo gedifferentieerd mogelijk leermiddelen aanbod' kan een dergelijke benadering vruchtbaar zijn. Zeer recent is er door Richmond op internet een publicatie neergezet over 'content assimilatie' (Richmond, op internet, 1998).
De combinatie van dit type leermiddelen en meer traditionele saaie instructiemiddelen kan een hele vruchtbare samenwerking tot stand brengen. Wij willen die discussie graag voeren aan de hand van een conceptueel model; een analogon. Immers dan weet iedereen waar we het - in kwalitatieve zin - over hebben en waar onze leer- en instructie-middelen in het gehele proces precies aangrijpen. We kunnen dan onderzoeksvariabelen en condities (kwalitatief) in kaart brengen. Later kunnen we ooit eens kijken of we er kwantitatieve gegevens over kunnen verzamelen.

Onderzoek naar modellen over leren is momenteel not done. Veel onderwijskundigen zien het belang er niet van in. Schmidt heeft recent (1998) een studie gedaan naar modellen. Hij stuitte op het 'modale model'. Dat model kent twee componenten: een component voor het korte termijn geheugen en een voor het lange termijn geheugen. Dit model baseert zich op (de volgens Schmidt onvolledige) ideeen over vergeten van Ebbinghaus (Schmidt, ORD'98 conferentie, 1998). Toch is er een behoefte aan een nieuwe start op dit gebied en een nieuw conceptueel model over leren.

Dit artikel beschrijft een basismodel over leren of, zo u wilt, een analogon. Het model is door de Universiteit Twente in samenwerking met anderen opgesteld. Dit model onderscheidt de afzonderlijke onderdelen en enkele veronderstelde basisprincipes zoals die bij leren en het leer-proces zijn te onderscheiden. Dit ruwe, eerste concept-model kan de discussie over leren en leermiddelen mogelijk stimuleren. Onderzoek naar leereffecten en een zinvolle wetenschappelijke discussie daarover is naar onze mening alleen maar mogelijk als op een eenduidige wijze de actoren en de dynamiek worden benoemd. Met een dergelijk model kan men duidelijk aangeven waar leermiddelen aangrijpen en waar bepaalde effecten hun uitwerking op hebben.

Instructie versus leren

Het model moet ook achtergronden vastleggen over hoe leren bij leermiddelen in zijn werk gaat. Wij hebben in de loop van jaren - terwijl we bezig waren met leermiddelen voor simulatie - ons een idee gevormd wat er met simulaties feitelijk bereikt wordt bij leerlingen: geen kennisoverdracht maar motivatie en 'zin gaan krijgen' in verdere studie over het onderwerp.

Theorie aangaande instructie ligt anders dan theorie aangaande leren. Deskundigen op het gebied van leren (de 'leertechnologen') hebben inmiddels goed onderbouwde denkbeelden die vaak haaks staan op denkbeelden uit de traditionele wereld van de instructie (de 'instructietechnologen'). Dat heeft natuurlijk alles te maken met het verschil dat instructie iets is qua aanbieden (de 'aanbodkant') en leren meer het door de gebruiker verzamelen van kennis. Dat is de 'vraagzijde' in het onderwijsveld. Het 'vragen om bepaalde informatie' en het 'aanbieden van informatie' zijn traditioneel, maar vooral ook ideologisch twee zeer verschillende wetenschapsterreinen. Vergelijk de ideeen van Gagné en Romiszowski maar eens met die van Van Parreren en Papert. Van Parreren en Papert hebben veel meer nagedacht vanuit het leren: het student-controlled leren. Uitgangspunten, benaderingswijze en de doelstellingen in hun oplossingen bij onderwijskundige problemen zijn behoorlijk verschillend t.o.v. de klassieke instructietechnologie.

In het wereldje van de onderwijskundige instrumentatietechnologie ('educational technology') zijn so wie so twee verschillende gebieden: de wereld van de 'learning technology' en die van de 'instruction technology'. In goed Nederlands: die van de leermiddelen-ontwerpers en die van de instructie-ontwerpers. Het is - in de hiervolgende analyses - zeer noodzakelijk om een strikt en goed onderscheid te maken tussen 'leermiddelen' en 'instructiemiddelen'. Leermiddelen bevatten in principe geen of niet veel kennis en instructiemiddelen wel. Als leermiddelen wel kennis bevatten dan is het feitelijk een combinatie van leer- en instructiemiddel. Of we moeten onderliggende modellen of systemen kennis noemen. Maar dat is hier niet aan de orde. Voor de goede orde: in de praktijk komt een combinatie dus wel veel voor. In dit betoog echter dienen die twee functies vooral los van elkaar bekeken en geanalyseerd te worden.

Ons idee begint met een goede indeling in soorten educatieve software naar soort. Men moet met name - om te beginnen - een goed onderscheid maken tussen leermiddelen en instructie-middelen. Het is namelijk zo dat leermiddelen geen instructie-middelen zijn. Leermiddelen zoals simulaties hebben als effect dat bij een goede casus de gebruiker een goede attitude krijgt aangaande het onderwerp en de 'lust' krijgt in een vervolgtraject: een les gaan volgen of een boek gaan lezen.

Stelling: Er is een groot verschil tussen leer-middelen en instructie-middelen

Stelling: Instructie-middelen zijn one-way omgevingen; leer-middelen zijn two-way omgevingen.

Een voorbeeld dat dit principiële verschil tussen instructie-rijk en instructie-arm duidelijk maakt is een kale practicumopstelling in een scheikundelokaal, waar afgezien van het lezen in een handleiding, geen kennisoverdracht plaats vindt. Daar tegenover staat een cursus op de televisie waar, op een bepaalde manier gedoseerd, wel kennis wordt overgedragen en weinig interactiefs aan is. Kortom dit zijn de twee uitersten: leermiddel versus instructiemiddel.

Als een simulatie goed werkt, raakt de gebruiker gemotiveerd voor een verdere studie in een (saai) boek of in een (saaie) vervolg-cursus. Leermiddelen moet men zien als werkomgevingen - net zoals practica - waar je leert omgaan met reeds verworven kennis en waar stukjes van een legpuzzel als het goed gaat en er goede casuistiek wordt gebruikt, als haast vanzelf, plotseling op de juiste plaats vallen. In ons model wordt instructie als een bron gezien vanwaar uit iemand kan putten; hier een 'stroombron'.

Stelling: Leermiddelen moeten motiveren tot echt leren en verdergaande studie

Het primaire doel van een leermiddel zoals een computersimulatieprogramma moet zijn motivatie voor eventuele verdere studie in saaie boeken of in saaie lessen. Leren komt bij ons type leermiddelen en simulatieprogramma's pas op de tweede plaats. Een computersimulatieprogramma moet het inzicht in de materie verhogen; moet grotere, ruimere verbanden leren zien; moet de samenhang tussen de dingen beter leren begrijpen; moet de reeds aanwezige kennis en inzichten verstevigen; moet de lerende conceptueler laten denken. In ons model hebben wij een onderdeel welke dit proces van motivatie simuleert. Als de motivatie nul is wordt er niks geleerd. Als de motivatie hoog is leert men heel snel.

Met computersimulatieprogramma's kun je 'leren door te doen'. Doordat je bezig bent met een taak of een casus leer je. Een simulatie omgeving is een 'doe'- en 'werk'-'omgeving' tegelijkertijd. Computersimulatieprogramma's en andere leermiddelen zijn van belang om een curriculum zodanig in te richten dat de leerlingen een gedifferentieerd leermiddelen aanbod krijgen aangeboden en waardoor een betere garantie ontstaat voor een individuele leerling dat hij een juist leer-traject kan doorlopen. Met een gedifferentieerd leermiddelenaanbod wordt de monotomie van een curriculum of een lesprogramma doorbroken. Een gedifferentieerd leermiddelenaanbod dient zuiver en alleen ter persoonlijke afwisseling (naar keuze) en omdat sommige studenten er op een of andere manier beter (wellicht door een andere benaderingswijze; bijvoorbeeld vanwege hun visuele of auditieve voorkeur voor het een of andere leermiddel) mee te motiveren zijn.

Het op gang houden van het leren: Door Min is in 1992 en 1994 reeds geopperd dat een goede instructie absoluut noodzakelijk is bij een kaal leermiddel, zoals 'gewone' simulatieprogramma's. Op zijn minst moeten er goede opdrachten of goede casussen bij een leermiddel als kale model-driven computersimulatie worden bijgeleverd.

In een van zijn artikelen poneert hij een stelling (als toetsbare hypothese) dat het leren met een leermiddel op gang moet worden gebracht door goede 'instructie' (teksten, plaatjes, instructie of video-instructies). En dat een goed gedimensioneerd leermiddel met goede feedback (tekstueel, grafisch en/of dynamisch) dat leerproces op gang moet weten te houden.

Onderstaande figuur geeft in feite het vereenvoudigde schema van bovenstaande complexe situatie weer. Deze figuur geeft aan dat een leerproces 'op gang wordt gebracht' door stimuli (allerlei vormen van instructies) en 'op gang wordt gehouden' door (allerlei) vormen van feedback, zoals 'messages', 'intelligente video fragmenten', 'groeiende grafieken', etc. (Zie Min 1992, 1994). Leren is duidelijk een feedback systeem waarbij 'netzolang geleerd wordt tot het gewenste nivo is bereikt'.

Figuur 4. Input en output voor een leerproces dat op gang gehouden 'moet' worden. Er is een input side en een output side bij een 'learning process'. On the input side of a learning environment a lot of instruction types and/or formats are possible and on the output side a lot of model-driven feedback forms are possible. Mijn stelling (hier) is dat als de juist 'instructie' wordt gekozen, het leren op gang komt. Als (vervolgens) door (hier) het leermiddel de juiste 'feedback' wordt gegeven, wordt het leerproces 'op gang gehouden'.

Stelling: Het op gang brengen van een leerproces (bij een inhoudelijk 'kaal' leermiddel) geschiedt (hoort te geschieden) door goede instructie (zoals opdrachten, boekjes, casussen, zelfinstructie, etc.).

Stelling: Het aan de gang houden van een leerproces (bij een inhoudelijk 'kaal' leermiddel) dient te geschieden door goede tekstuele en grafische feedback.

leermodellen: Min heeft in 1992 een pilot-onderzoek gedaan naar 'leermodellen' bij computersimulatie. Het begrip 'leermodel' is niet het zelfde als een 'model voor leren'. Het begrip is door hem voor iets heel anders gereserveerd; daarom gebruiken we in dit artikel systematisch de omschrijving: 'een model voor leren' of nog beter 'een model aangaande leren'. (Min, 1992.) Hij onderscheidde toendertijd vijf (mede door onderzoek verkregen) 'onderwijskundige soorten van gebruik' van (model-driven) simulatieprogramma's en dientengevolge dus ook vijf 'soorten van leren'. Die modellen werden leermodellen genoemd. (Zie elders.)

Die vijf te onderscheiden leermodellen werden opgesteld aan de hand van observaties van leergedrag. Die experimenten zijn gedaan in de observatieruimten bij Toegepaste Onderwijskunde. De experimenten werden met drie video camera's vast gelegd. Er werden twintig proefpersonen gebruikt. De analyses van de tapes hebben uiteindelijk een jaar geduurd. De kwalitatieve leermodellen konden daardoor uiteindelijk worden omgezet in kwantitatieve leermodellen. Op de data is door studenten, later (in 1996), ook nog een patroonherkennings-studie uitgevoerd. Die studie leidde tot nuttige resultaten, maar is nog lang niet uitputtend geweest. In 1991 heeft hij op het 'Gezond Onderwijs Congres', dat ieder jaar georganiseerd wordt door de Nederlandse Vereniging voor medisch onderwijs, daarover gerapporteerd (Min, 1992)

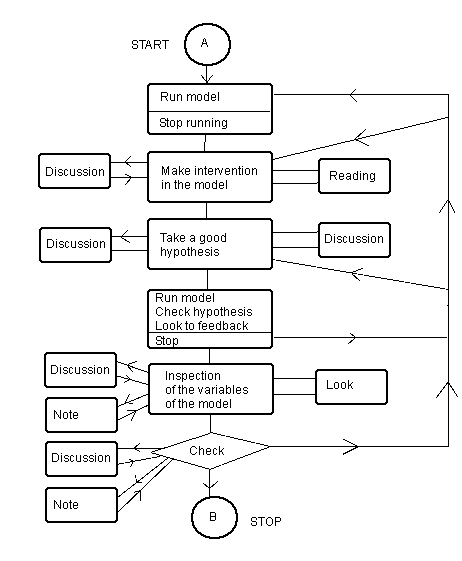
Figuur 5. Een van de vijf 'leermodellen' van Min (1992) voor "a qualitative idea how pupils learn in simulation learning enviroments". Te zien is dat bij 'leermodellen' van Min ook feedback-loops een rol spelen. We komen daar in de conclusies op terug.

Toch kunnen we ons niet aan de indruk onttrekken dat er overeenkomsten zijn met de bevindingen van toen, en de bevindingen van nu, bij dit project over het opstellen van een analogon van leren. We hopen de overeenkomst tussen die twee benaderingswijzen later toch nog eens te kunnen leggen. Voorals nog zien we het als twee gescheiden opvattingen. Indien we het leggen naast de ideeen dat stroomschema's eigenlijk feedback systemen zijn - en dat kunnen we aantonen - dan moet een dergelijk overeenstemming heel goed te bereiken zijn. Zie daarvoor de afbeeldingen en de leesteksten in het onderwijsmateriaal van het vak 'Systeembenadering in de Onderwijskunde' van Vos en Min (Vos en Min, 1997)

Definitie: Een leermodel (niet te verwarren met 'een model voor leren') is (bij Min, Gezond Onderwijs Congres, 1992) een stroomschema waarin het gedrag van een lerende welke gebruik maakt van een simulatieprogramma kan worden vastgelegd (maar niet verklaard).

Er zijn volgens Min vijf of zelfs zes typen leermodellen behorende bij de vijf of zes verschillende soorten gebruik van simulatieprogramma's als leermiddel. Leermodellen en het hier beschreven 'model van/voor leren' blijken achteraf gezien een aantal sterke overeenkomsten te hebben; zodanig dat verdere studie noodzakelijk is om beiden mogelijkerwijs in elkaar te kunnen laten overvloeien. Zie de conclusies.

Een weerstands-netwerk als model

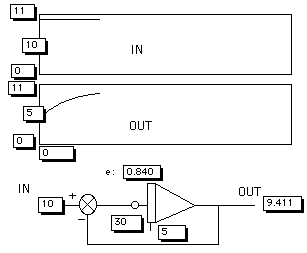
Figuur 6a. Het hart van het analogon - de overdrachtsfunctie van input naar output - gesimuleerd op een PC. De overdrachtsfunctie van dit model is van het type du/dt = 1/RC (E-u). U dient te beseffen dat e=E-u. Hier e=IN-OUT. De integrator gaat net zolang door met integreren tot e=0. Op dat moment is u=E of OUT=IN. Dit model kan dus model staan voor kennisvergaring. Het programma LEREN versie 1. Zie elders.

Figuur 6b. Een iets uitgebreider model voor kennisvergaring. Het programma LEREN, versie 2. U ziet in dit simulatieprogramma, waar het model voor leren in verwerkt is, dat er een aantal doelen zijn die leerlingen zich zelf kunnen stellen. Men komt dan uit op een bepaald kennisniveau. Men begint op niveau 5 en men kiest doel (of niveau) 6, 7, 8, 9 of 10. In dit voorbeeld heeft men op diverse tijdstippen steeds een hoger doel gekozen. (Het beginniveau van de leerling was 3.) U ziet dat de leerling de niveaus na een zekere tijd bereikt.

Wij hebben ons 'leer-model' in eerste instantie (in 1994) als een schakeling van een condensator met een weerstand opgevat. Een RC-netwerk is in onze optiek een goed analogon voor de basisprincipes in het spanningsveld tussen leren met een leermiddel en het gebruik van een instructeur daarbij. In deze schakeling is de condensator de leerling. De 'capaciteit' van een condensator is te vergelijken met verstand, geheugen of intelligentie. Het leren is daarmee te vergelijken met het opladen van een condensator C. Als de capaciteit groot is, is het leervermogen ook groot. Als de capaciteit C klein is, is het lerend vermogen ook klein.

De leerling heeft als 'natuurlijke' grondhouding een zekere weerstand tegen leren. Dat is de weerstand R1. Zowel het 'zelf ontdekkend willen leren' als het 'geinstrueerd willen worden' gaat moeizaam. Bij een leermiddel kan een mondelinge instructie zitten, maar ook een instructieboekje of een bepaalde opdracht kan niet duidelijk overkomen. Die weerstand daartegen kan door een goed ontworpen (of 'aaibaar') leermiddel worden verminderd. De weerstand die een leraar of een instructeur of een instructieboekje bij een leerling ondervindt wordt gerepresenteerd door de weerstand R1.

Figuur 7. 1e type analogon: een condensator. De leerling heeft (een) bepaalde capaciteit en wil leren. Het willen onthouden (en dus leren) wordt voorgesteld door een condensator C; met een bepaalde opname-capaciteit. U is het aanbod: de stof (uit een boek) of de instructie (uitgesproken door een docent). Het aanbod, de instructie, de stof is een 'spannings'-bron of een 'stroom'-bron. Dat maakt in principe niet uit. De overdrachtsfunctie hierbij is van het type du/dt = 1/RC (E-u).

De instructie of een instructie-middel wordt in ons model als een spanningsbron (U) of een stroombron opgevat. De vraag hierbij is of de leerling ontvankelijk voor de instructie is. De weerstand R1 representeert die weerstand of de weerzin tegen leren. Deze weerstand of weerzin tegen leren is meestal hoog. En tevens is er mee aangegeven dat leermiddelen - zoals simulaties - aangrijpen bij R1. De weerstand tegen instructie, lezen, lessen volgen wordt minder. Na het volgen van een paar sessies met simulatieprogramma's - zo is onze stelling - is de leerling meer ontvankelijk voor het volgen van lessen of instructie. De 'vraag' naar leren is gestegen. De leerling 'schreeuwt' als het waren om informatie en/of instructie. Hij is meer bereid 'moeilijke trajecten af te leggen' en boeken te lezen over het onderwerp waar de simulatie over ging, dan daarvoor. R2 is de lekweerstand die het vergeten representeert.

Figuur 8. 2e type analogon: een feedback regelsysteem. Dit is in principe het achterliggende systeem bij leren zoals Scheiblechner, en Vos en Min het in hun colleges bij het vak 'Systeembenadering in de Onderwijskunde' (1997) beschrijven. De leerling krijgt een stimulus aangeboden en gaat net zolang door tot het verschil tussen de 'kennis in de stimulus' en de 'kennis in zijn hoofd' nul is. Het verschil in een feedback systeem gaat altijd naar nul. De curve die daarbij hoort komt op vele plaatsen in de sociale wetenschappen, de psychologie en de natuurkunde voor. In werkelijkheid is er een veelvoud van stimuli. (Zie verderop in de tekst en bij de figuren.) Maar ook een veelheid van 'doelen' en 'feedback systemen'. Maar de som van al deze activiteit en kennisaccumulatie is dus 'leren'. Als men zich meerdere doelen ('leerdoelen'; 'goals'; etc.) stelt, dan kun je spreken van dynamische doelen of normen. Bij enkelvoudige doelen (of normen) kun je (blijven) spreken van een statisch doel of een norm.

Figuur 9. Idem, als hierboven. Deze voorstelling komt overeen met de voorstelling zoals Atkinson (1977) geeft in zijn leervergelijking. Zijn model geeft een voorstelling hoe de leer- of kennistoename bij een leerling zou kunnen verlopen in de tijd gegeven een stimulus b: de totaal te leren hoeveelheid materiaal. Zie ter vergelijking ook het model van de 'diffusie'-vergelijkingen in het broadcast-model van Lave & March (1975).

De tweede weerstand - (R2) parallel aan de condensator - is de 'lekweerstand' over de condensator en symboliseert het 'vergeten'. Het goede gebruik van het leermiddel maakt de weerstand tegen verder leren minder en grijpt dus aan op de weerstand R1. Een goede instructie bij een leermiddel is belangrijk om het leerproces op gang te brengen. Deze wordt gesymboliseerd door de spanningsbron (U). Het model voor hoe het leren onder invloed van het leermiddel en de instructie in zijn werk gaat is in de figuren in de tekst goed te zien. Hiermee is dit analogon een bruikbaar kwantitatief model voor leren geworden.

Samenvattend kunnen we een aantal zaken die van belang zijn bij het leerproces, bij kennisoverdracht of bij kennisverwervingsproces en hun analoge componenten tegenover elkaar zetten:

• instructie als een stroom of spanningsbron (U);
• de kennis accumulatie - het leerproces - als een feedback systeem of als een condensator (C);
• communicatie als een stroom (i);
• weerstand tegen leren (d.w.z. 'motivatie') als een weerstand (R1);
• studeerbaarheid als een weerstand (in serie) (R3);

De wet van Ohm geldt hier dan ook. Dat ligt voor de hand. Dus U=i.R. Als 'een weerstand' afneemt of 'motivatie verhoogt' dan gaat het leren beter. De weerstand tegen leren (d.w.z. 'motivatie om te leren') (als functie van R1 of beter 1/R1) kan voor een deel worden weggenomen door goede leermiddelen. De studeerbaarheid (als functie van R3 of beter 1/R3) kan toenemen door een goed en gestroomlijnd management in het curriculum en een adequaat en specifiek instructie- en leermiddelen aanbod. Als de studeerbaarheid toeneemt en (hier) de weerstand R3 afneemt dan wordt in potentie het leren makkelijker. De wet van Ohm zegt dat bij een gegeven spanning (U) de stroom (i) toeneemt als de weerstand (of een van de weerstanden in serie) afneemt.

Stelling: Studeerbaarheid is (volgens de commissie Wijnen) de taak van de universiteiten om de student snel en goed te kunnen laten omgaan (met zijn schaarse tijd, onbegrijpelijke roosters, onbegrijpelijke leerteksten en leermiddelen) en leertrajecten niet moeilijker te maken dan ze zijn.

Stelling: Een weerstand tegen leren komt voor als er onnodige barrieres voor komen in een studietraject. Aanbieders van onderwijs en leermiddelen ontwerpers dienen de weerstand tegen (hun) onderwijs en (hun) leermiddelen bij voorbaat zo klein mogelijk te maken of te houden.

Anderson (1983) geeft in zijn ACT-model ('adaptive control of thought') de betrekking aan hoe kennis (zowel declaratieve als procedurele) geactiveerd wordt in semantische netwerken, bestaande uit knopen en bronnen, of te wel hoe kennis diffundeert. Het onderscheid met ons model is dat er geen sprake is van een (spannings-)bron, maar van meerdere bronnen en invloeden (bijvoorbeeld ook leer-doelen) die met elkaar in interactie staan en elkaar activeren, waardoor complexe overdrachtsprocessen mogelijk worden gemaakt en in een model kunnen worden gevat. Wiskundig betekent dit dat we te maken krijgen met matrices. Dit zullen we in dit artikel niet verder uitwerken.

Een kwalitatief model (een analogon) over hoe instructie en kennisopname in hun werk gaan, kan dan middels het model gevisualiseerd en 'gedynamiseerd' weergegeven worden. Zie figuur 5.

Figuur 10. Studeerbaarheid staat in dit model in serie met motivatie. Hoe hoger de studeerbaarheid, d.w.z. hoe lager de weerstand (R1), hoe beter er geleerd kan worden. Hoe hoger de motivatie, d.w.z. hoe lager weerstand (R2), hoe beter iemand nuttige zaken (kennis, informatie, inzicht en wellicht wijsheid) in zich opneemt. En omgekeerd: hoe hoger weerstand R1 en R3 (in serie) zijn, hoe slechter er geleerd wordt. Simulaties verhogen de motivatie voor het leren van ongeveer dezelfde stof uit boeken. R1 en R3 staan in serie en versterken elkaar. Dat klopt met de werkelijkheid: studeerbaarheid en motivatie dienen bij elkaar opgeteld te worden. De vervangingsweerstand bij weerstanden in serie is gelijk aan R1+R3.

Figuur 11. Een groot (en 'gedifferentieerd') (leermiddelen-)aanbod. Hier is aangegeven dat een leerling zelf instructiemiddelen of kennisbronnen kiest. Het aanbod is groot. De weerstand tegen het ene (bijvoorbeeld tegen de studeerbaarheid) is hoger of lager dan tegen het andere instructie- (of leermiddel).

De weerstand die een leraar of een instructeur bij een leerling ondervindt wordt gerepresenteerd door de weerstand R1. De tweede weerstand R2 is de 'lekweerstand' over de condensator en deze symboliseert het vergeten. Daar heb we een nederlandstalig artikel over gevonden. Dit artikel van Meerling van de Universiteit Leiden (1981) handelt over een model (uit 1880 !) van Ebbinghaus en legt het accent sterk op het 'vergeten' en niet zo zeer op 'leren'. Zijn model is dan ook een 'kwantitatief' model (empirisch onderbouwd) voor vergeten dan een 'kwalitatief' model voor leren; laat staan een analogon voor leren. Ebbinghaus modelleert de (zogenoemde) 'vergeetcurve' als pn=p1(1-a)^n-1, waarbij pn het percentage foute responsies representeert bij de n-de trial; p1 de voorkennis en a bijvoorbeeld weer de intelligentie (Meerling in: H. Vos, collegediktaat,1997). Naar onze mening staat het kwantitatieve benaderings-onderzoek momenteel min of meer stil. Blijkbaar moet er eerst een meer compleet kwalitatief model worden opgezet. Zijn artikel suggereert een bepaalde nauwkeurigheid, die er naar onze mening op deze manier niet is. Zeker niet in dit stadium van modelvorming over leren. Het is wel tijd voor een kwalitatief model.

Discussie

We zullen drie modellen in de discussie betrekken: (1) de leermodellen van Min, (2) het hier voorgestelde denkmodel van leren van Min, Kommers, van Dijkum en Vos, en (3) een (nieuwe) 'kijk op ontwerpen' (een ontwerpmodel) We zullen aantonen dat er een grote verwandschap tussen deze drie 'modellen' is.

Leer-modellen: De leermodellen van Min zijn reeds in 1995 opgezet. Pas in 2000 werden pas de eerste eindconclusie duidelijk. In eerste instantie beschreef hij de leermodellen kwalitatief van aard; in tweede instantie probeerde hij deze om te zetten naar kwantitatieve modellen met echte, gemeten gemiddelde waarden van bijvoorbeeld het aantal malen welke iemand een lus doorloopt tot en met de (gemiddelde) verblijftijden.

Ons model voor leren: Het model van leren wordt gekenmerkt door een integrerend systeem. We kunnen daarvoor het beste als analogon de teruggekoppelde integrator nemen. Dat model fit redelijk en maakt het mogelijk om relaties te leggen met motivatie en studeerbaarheid. En daar was het ons (immers) steeds om te doen. Het model met de condensator - hoe goed passend en eenvoudig ook - moeten we zien te vermijden om overbodige discussies te voorkomen.

Ontwerpmodellen: Figuur 14a, links, laat zien dat ontwerpen ook iets dergelijks kent en derhalve is daar ook een model dat sterk hier op lijkt op te stellen. Een model voor ontwerpen dat ook tevens de ontwerpcyclus beschrijft; een 'analogon' voor ontwerpen. Een onderwijskundige oplossing kent - als het goed is - altijd een 'meetmoment' (de evaluatie) en een terugkoppellus die zo vaak wordt doorlopen tot dat de gemeten waarde gelijk is aan de gewenste waarde (b). Een ontwerper wil (ook) een verschil van nul tussen de gewenste waarde en de gemeten waarde.

Figuur 13. Het niveau van de kwaliteit van een product groeit ook in de tijd. Het OKT-model kent een feedback-lus waarbij de evaluatie (het 'meten') het belangrijkste onderdeel is. Als je een evaluatie inbouwt - hoe klein en eenvoudig dan ook - vrijwaar je jezelf tegen risico's zoals bij een feedback-loos systeem zoals een feedforward-systeem wel bijna altijd een probleem is. Feedforward systemen zijn in de praktijk volkomen onhanteerbaar als er storingen of tegenvallers om de hoek komen kijken. Als de gemeten kwaliteit gelijk is aan de gewenste kwaliteit is het product af of de oplossing in orde. (Zie de literatuur over de theorie van Quality Control, o.a. Juran, 1962 (eerste druk) en Bush & Mosteller, 1955)

Figuur 14a (links) en b (rechts). Een overeenkomstig regelsysteem. Ook het OKT model kent principieel dezelfde regelkring zoals ook in ons model van leren zit. Het ontwerpen kent/heeft een soortgelijke dynamiek als het leren. (Accumuleren van kennis versus het accumuleren van kwaliteit van een product? (Einddoelstelling - target - gehaald?) Als jet het OKT model (links) een kwartslag draait is het een feedback systeem met een 'meetmoment' (de evaluatie) en een terugkoppellus die zo vaak wordt doorlopen tot dat de gemeten waarde gelijk is aan de gewenste waarde (rechts). Een ontwerper wil (ook) een verschil van nul. De ontwerper gaat zet zolang door met het bijschaven van zijn product of oplossing tot het gewenste resultaat ('goal' of 'target') is behaald. Daar is 'e=0'. De ontwerper 'stopt' dan met zijn ontwerp; het ontwerp is 'klaar'.

Figuur 15a. Ontwerpen als een feedback systeem

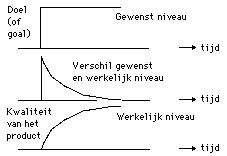
Figuur 15b. De drie belangrijkste curves zijn: boven: het 'doel' ('goal' of 'target') dat men zich - in het begin stelt. Midden: het verschil tussen de gewenste waarde en de werkelijke - gemeten - waarde. Onder: de 'kwaliteit' van het product.

Verder onderzoek moet uitwijzen of dit model een plausibele verklaring kan bieden voor een aantal fenomenen die juist in samenhang zo belangrijk zijn om begrepen te worden. Dit om de spraakverwarring over begrippen, actoren en effecten mede te helpen oplossen.

Conclusies

Enschede, 1996-1999; updated 2005.

Referenties

Bush, R.R. & F. Mosteller (1955)
Stochastic model for learning. Uitg.: Wiley & Sons, Inc, New York; Chapman & Hall, Limited, London. (copie bij de auteurs; ingezien bij MIT, Cambridge, USA)

Ek, M., F. Gooters, C. v.d. Leest and J. Olde Achterweg (1995) Het opstellen van kwantitatieve 'leermodellen' bij simulaties / Kwantitative and kwalitative 'learning models' in learning environments) OKT verslag / Rapport. University of Twente (Begeleiding/Supervisor: Rik Min)

Juran (1962 eerste druk)
Quality Control. MIT, Cambridge, USA.

Groenewoud, U.A., J. ter Burg (1996)
Effect van mate van parallellisme op taakuitvoering en gepercipieerd gebruiksgemak. Een onderzoeksverslag, gebaseerd op empirisch onderzoek. Faculteit Toegepaste Onderwijskunde, Universiteit Twente. M.m.v.: W. Akkermans (methodoloog) en R. Min (begeleiding/supervisie). (Ook gepubliceerd op Internet.)

Min, F.B.M. (1996)
Parallelism in working-, learning- and doing-environments; The Parallel Instruction Theory for Coaching in Open Learning Environments for Simulation; Proceedings of EuroMedia 96; Telematics in a multimedia environment, dec.19-21, 1996; A publication of the Society for Computer Simulation International (SCS) (Eds. A. Verbraeck & P. Geril)

Min, F.B.M. (1995)
Simulation Technology & Parallelism in Learning Environments; Methods, Concepts, Models and Systems. Publisher: Academic Book Center, De Lier. ISBN 90-5478-036-3

Min, F.B.M. (1994)
Parallelism in open learning and working environments. Britsh Journal of Educational Technology, Article; Vol. 25, No. 2, pp. 108-112. ISSN 0007-1013.

Min, F.B.M., (1992)
Parallel Instruction, a theory for Educational Computer Simulation. Article. Interactive Learning Intern., Vol. 8, no. 3, 177-183.

Min, F.B.M., (1992)
Pilot-onderzoek naar 'leermodellen' bij computersimulatie aan de hand van observaties van leergedrag; Paper in proceedings van 'Gezond onderwijscongres' door de Nederlandse Ver. voor medisch onderwijs in samenwerking met de vakgroep Onderwijsontwikkeling en Onderwijsresearch, Rijksuniversiteit Limburg op 28-29 november1991 te Velthoven. Redactie: C.P.M. van der Vleuten, A.J.J.A. Scherpenbier en M.C. Pollemans; Uitgever: Bohn, Stafleu Van Loghum BV. Houten. pag. 130-137. ISBN 90-313-1489-7.

Min, F.B.M., H. Vos en P. Kommers (1998)
Voordracht; Rijsuniversiteit Utrecht.

Spada, H. & W.F. Kempf (Eds.) (1977)
Structural Models of Thinking and Learning. Proceedings of the 7th IPN Symposium on Formalized Theories of Thinking and Learning and their implications for science Instruction. Hans Huber Publ., Vienna.

Vos, H. en Min, R, (1997)
Systeembenaderingen in de onderwijskunde, Studiehandleiding, TO/Universiteit Twente, Enschede, (cursusjaar 97/98)

Vos, H. (1997)
Methodenleer, Syllabus, TO/Universiteit Twente, Enschede, (cursusjaar 97/98)

Enschede 1996 - 2000. Gerestaureerd in 2020.