
MULTIMEDIALE LEERMIDDELEN --- LOS TEKSTFRAGMENT
Systeem-denken, control theory, regelsystemen en feedback
Deze tekst gaat over: systemen, systeemleer, control theory, besturingssystemen, systeem dynamica, regelsystemen, input, output, feedback, terugkoppeling, 'gemeten' waarden, 'gewenste' waarden en het verschil daartussen, comparator, homeostase, systeem-denken vs. machine-denken, open en gesloten systemen, black box, blok-diagram, oorzaak-gevolg-relaties, causaal denken, cybernetica (oude term), systeemtheorie (betere term), (wiskundige) modellen als concepten van een stukje werkelijkheid, meekoppeling versus tegenkoppeling, feedback loops, stabiliteit, steady state, regelsystemen, stimulus-respons-gedrag, gedragsonderzoek, stochastische systemen, waarschijnlijkheden, etc.
Er bestaat bij psychologen, communicatiewetenschappers en onderwijskundigen veel onduidelijkheid over besturingssystemen, interne regelsystemen in het menselijk lichaam, de rol van de hersenen, feedback en het uiteindelijke gedrag van wat we dan noemen control systems. Hier doen we een poging dat systeem-denken en denken in termen van feedback wat op te helderen voor studenten uit de gedragswetenschappen.
We kunnen ons aangaande gedrag van systemen, het besturen, controleren of regelen van systemen de volgende vragen stellen:
- Wat is een control system?
- Wat is een regelsysteem?
- Wat is een besturingssysteem?
- En wat is het verschil daar tussen?
- Wat voor soorten systemen zijn er in dit vakgebied (en elders)?
- Is een besturingssysteem een regelsysteem?
- Wat is feedback?
- Heb je altijd feedback nodig?
- Zijn feedback loops gemakkelijk te herkennen?
- Waar, en in welke wetenschapsgebieden komen dit soort systemen voor?
- Waar moet je op letten bij dit soort systemen?
- Wat is homeostase?
- Wat is het verschil tussen deteministische en stochastische systemen?
- Wat zijn kenmerken van oorzaak-gevolg-systemen?
- Wat zijn kenmerken van stimulus-respons-systemen?
- Hoe kan 'het brein' variabelen meten en constant houden?
- Wat is het nut van systeem-denken?
Let op: Deze pagina bevat 'micro-werelden' voor educatieve doeleinden: applets, d.w.z. kleine 'intelligente' software applicaties. In deze interactieve werk-, ontdek- en/of leer-omgevingen kun je binnen bepaalde grenzen - online - je eigen of andermans ideeen over de stof uitproberen.
Soorten systemen
We hebben het hier met name over systemen waarmee 'iemand iets kan doen': die een aktie veroorzaken omdat iemand er iets mee wil en doet, dat wil zeggen: systemen die een output hebben als er input is. Systemen die je kunt instellen, besturen of die iets voor een gebruiker regelen. Er bestaan volgens Kramer en De Smit in hun boekje 'Systeem-denken' (1990) twee fundamentele soorten van deze systemen: feedforward systemen en feedback systemen. De eerste systemen hebben geen feedback en er is geen controle achteraf of tijdens het sturen of besturen. De tweede soort systemen kenmerken zich door een permanente controle: of het doel wat ik instelde, wel gehaald wordt. Dat zijn dan systemen waarbij steeds - zoals dat heet - feedback wordt gegeven. We noemen dat feedback systemen of systemen met feedback. U ziet hieronder, in twee figuren, de kenmerkende verschillen. Het ene systeem heeft geen feedback; het andere wel. Deze systemen komen overal voor; ze zijn soms technisch, maar zitten ook in het menselijk lichaam of liggen ten grondslag aan ons handelen. Een wetenschapper moet ze zien zitten en kunnen onderscheiden.
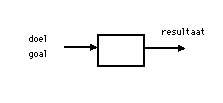
Figuur 1. Een feedforward systeem. Een dergelijk systeem geeft output als er input is. Iedere 'oorzaak' heeft een 'gevolg'. De output is (sterk) afhankelijk van storingen.
Als je iets wilt in een systeem waarbij geen feedback is, moet je maar afwachten of je doel bereikt wordt en dat het resultaat wat je wilt bereiken het juiste is (geworden). Bijvoorbeeld blind een draai aan het stuur van je auto geven. Bij feedback systemen wordt door het systeem de waarde van het resultaat - op een of andere automatische manier - steeds vergeleken met de gewenste waarde. Zoals het instellen van de kamertemperatuur bij een centrale verwarming: je hoeft er niet bij te blijven staan of de temperatuur wel keurig op de gewenste waarde komt. Daar kun je namelijk gewoon op rekenen. Er is een feedback systeem. Bij een blinde draai aan het stuur van een auto niet.
Voorbeelden van feedforward systemen zijn:
- Een pijl uit een boog afschieten. U wilt een pijl van A naar B schieten. Als er een plotselinge wind opsteekt kan de pijl ergens anders (neer)komen dan de schutter voor ogen had. De wind is dus een storing voor dit systeem van pijlen afschieten. Na het vertrek van de pijl uit de boog heeft niemand meer invloed op de pijl.
- Een gaspedaal van een auto indrukken. Bij een bepaalde stand van het gaspedaal veroorzaakt een helling dat de auto zachter gaat rijden. Bergafwaarts gaat de auto dan juist harder rijden. Beide situaties zijn niet gewenst. De hellingshoek is te zien als een niet te voorspellen zaak en dus een storing.
- Domweg een eindexamen voorbereiden. Domweg 20 weken achter elkaar lessen volgen en studeren zonder te kijken wat de resultaten zijn. Zonder feedback. Dan werk je te hard of te langzaam en kan het resultaat wel eens erg tegen vallen. Studenten zowel als docenten kunnen deze fout maken.
- Domweg kinderen opvoeden. Domweg kinderen iets vertellen c.q. instrueren en niet c.q. nooit naar hun resultaten kijken of hen een toets afnemen. Bijvoorbeeld alle kinderen in een klas een jaar lang volstoppen met van alles en - als je ze nooit tussentijds toetst - na een jaar verwachten dat ze allemaal hetzelfde en alles allemaal even goed hebben geleerd. Als er gedurende een jaar geen tussentijdse feedback is geweest kan het resultaat op het einde van het jaar natuurlijk zwaar teleurstellen.
Bij al dit soort systemen moet je maar afwachten wat het resultaat van je aktie of inspanning is. Ook moet je maar afwachten wat er bij een kleine of grote tegenslag - gedurende de ongecontroleerde aktie - met je eindresultaat gebeurd. Daarom zijn er feedback systemen.
Bij de stoommachines kwam het vroeger wel voor dat de ketels explodeerden als je te veel kolen op het vuur gooide of als de stoker, na een lange periode van oplettendheid, even niet oplette. Toen de regulator werd uitgevonden kon men in ieder geval het toerental constant houden (de Watt-regulateur, Maxwell, 1868).
a. 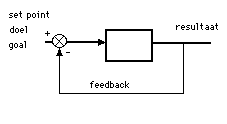
b. 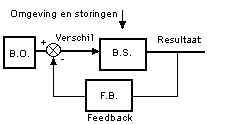
c. 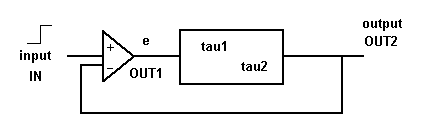
Figuur 2a, b en c. Een feedback systeem op drie verschillende manieren weergegeven: a, b en c. Een feedback systeem geeft 'output' als er 'input' is (hier: 'resultaat').
Binnen het kale onbestuurde bestuurd(e) system (B.S.) heeft iedere 'oorzaak' een 'gevolg'. Het B.S.-blok is feitelijk (gewoon) een feedforward systeem. De gevolgen en de snelheid waarmee dat gaat, hangen af van zogenaamde tijdconstantes. Hier aangegeven met 'tau1' of 'tau2'. Maar bij een teruggekoppeld systeem hangt de output ook nog op een andere manier van dingen af. Als namelijk de 'gemeten waarde' (van de output) veel afwijkt van de 'gewenste waarde' (de input) stuurt het systeem 'harder' of 'sneller' dan als dat verschil tussen output en input weinig is. De output is (in principe) niet afhankelijk van storingen.
In het dagelijks leven, in de techniek, maar ook in de bestuurskunde, de bedrijfskunde, de communicatiekunde en de psychologie kom je veel feedback systemen tegen. De natuur zelf zit vol met allelei soorten systemen met allerlei soorten feedback: meestal 'tegen'-koppeling en soms 'mee'-koppeling; maar altijd een van deze soorten terugkoppeling (Kramer en De Smit, 1991). Voorbeelden van feedback systemen zijn:
- Centrale verwarming. U stelt de temperatuur op 20 graden in en ongeacht of het vriest of dat er een storm met een zware regenbui langs komt, blijft de temperatuur in huis 20 graden. Verstoringen door storm, regen, het openen van een raam of het aanzetten van een open haard, worden opgevangen door dit automatische regelsysteem. Dit soort regelsystemen houden bepaalde variabelen constant. Dat automatisch constant houden van output noemen we 'homeostase'. Deze toestand van (relatieve) stabiliteit noemen we 'steady state'. De steady state is meestal de ingestelde waarde van de input; hier de termostaat die op 20 graden is gezet.
- Lichaamstemperatuur. De lichaamstemperatuur wordt door metabolisme op 37 graden Celcius gehouden. Ongeacht of je in koud water zwemt of in de woestijn loopt, de temperatuur van je lichaam blijft altijd rond de 37 graden schommelen. Ook hier: homeostase is zeer belangrijk in het menselijk lichaam. Er zijn vele voorbeelden van te geven. De steady state van dit systeem is (hier) 37 graden Celcius. Het set point is hier dus 37 graden.
- Kruisraket. Ongeacht zijwind vliegt een dergelijk projectiel op zijn doel af; ook al wordt hij niet precies in de richting van het doel gelanceerd. Tijdens de vlucht wordt voortdurend op een soort radarscherm en een digitale landkaart gekeken of hij de goede richting op gaat. Zo niet dan worden de stuurraketten anders ingesteld. Als de afstand tussen de gewenste waarde en gemeten waarde nul is dan ontploft de bom. Als dit niet het geval is, dan vliegt de raket net zolang door tot dat wel het geval is of totdat de kerosine op is.
- Parkeren. Parkeren door te botsen en te luisteren. U parkeert door te 'luisteren' of er nog ruimte is tussen u en uw buurmans auto. U wacht op feedback door er zachtjes tegen aan te rijden. Dat geeft auditieve feedback. Uw oren pakken dat signaal op en u reageert door aan het stuur te draaien, de andere kant op te rijden of door gas terug te nemen.
- Honger- of dorstgevoel. Het honger- en dorstgevoel zijn regelsystemen. Ze houden de vochtbalans in de gaten. Als iemand te weinig drinkt of eet dan geeft het lichaam - op een of andere manier - signalen af waardoor de persoon dit tekort op een bepaald moment weer bij gaat vullen. De momenten zijn willekeurig. Dit soort systemen hebben naast hun deterministische aard en aanleg altijd een stochastisch element; de input heeft een 'at random' gedrag; eten en drinken vind altijd plaats op een onbepaald, in principe willekeurig moment.
- Insuline huishouding. De insuline/glucose regulatie in het menselijk lichaam is een regelsysteem. Dat heet de insuline huishouding. Normaal verloopt deze 'huishouding' automatisch. Als iemand teveel glucose in zijn bloed heeft dan heeft dat iets te maken met het set point c.q. de instelling of de verstoring van een regelsysteem. Ook dit systeem is grotendeels een stochastisch systeem.
- Verslaving. Veel vormen van verslaving hebben op een of ander manier te maken met feedback-loops. Een volkswijsheid zegt: Het lichaam is (soms) sterker dan de geest. Hoe verslaving werkt en waarom het lichaam dominanter is dan de wil om van iets af te komen, is (nog) erg onduidelijk. Het heeft iets te maken met het set-point van een regel mechanisme en de verschuiving daarvan.
- Neurologisch voorbeeld 1: patient niet verlamd. Loopt onzeker. Begint iedere stap met een schok
Werpt been naar achter en naar voren.
- Neurologisch voorbeeld 2: patient zit rustig in een stoel. Bij aanbieden van een sigaret schiet zijn/haar hand mis. Steeds weer.
Bij beide patienten is signaalstroom verstoord die de terugkoppeling verzorgt waarmee de bewegingen worden beheerst.
Het 1e geval is een ruggenmerg-aandoening. Signalen (qua stand en positie) uit de benen en de voeten bereiken hersenen niet.
Het 2e geval is een storing in (een deel van) de hersenen. Mate van reactie (van de spieren) niet juist afgestemd op de grootte van de afwijking.
- 'Quality control' systems. Dit soort systemen komt veel voor in de bedrijfskunde. Japan was na de Tweede Wereldoorlog het eerste land dat dit principe van 'kwaliteitscontrole' overal serieus toepastte (Juran, 1946). De kwaliteitscontrole systemen van Juran hebben tegenwoordig in alle bedrijven veel betekenis. Dit soort systemen zijn feedback systemen waarbij de kwaliteit van een product of een proces constant gehouden kan worden door goede instelling (hier genoemd 'set point', 'target', 'goal', 'plan', of de waarde van 'B.O.' of 'IN') inclusief een voortdurende controle: door steeds de waarde van een (bepaalde) output-variabele (hier bijvoorbeeld 'OUT') te meten en die waarde te vergelijken met de gewenste waarde (via + en - in het vergelijkende element). Dit noemt Juran 'kwaliteitscontrole'. Is de 'kwaliteit' van de output (bij de meeting) slecht, dan moet het productieapparaat beter ingesteld worden. Juran gaat uit van drie belangrijke grootheden voor quality control: planning en controle, met als resultaat: de voortdurende verbetering. In alle fasen van een productieproces moet er volgens hem controle zijn. Dan krijg je een stabiele kwaliteit en kun je veranderingen in de 'kwaliteit van de output' uitsluiten.
- De wet van 'behoud van reistijd'. Het blijkt uit onderzoek naar reistijden bij forenzen dat iemand steeds verder van zijn werk gaat wonen als zijn of het (openbaar) vervoer beter is/wordt. Hoe komt en hoe werkt dat?
- De wet van het 'behoud van een veiligheidsgevoel'. Het blijkt uit onderzoek naar snelheden bij automobilisten dat iemand die veiligheidsgordels om heeft toch (onbewust) systematisch harder gaat rijden. Hij waant zich blijkbaar veilig. Hoe dat soort 'aanpassing' (van het set point) precies werkt, moet nader onderzocht worden.
- Conditionering. Conditionering is op een of andere manier ook een gecontroleerd systeem. Het menselijk brein speelt hiereen rol; en hoe men met targets omgaat. In het verleden is hier veel onderzoek naar verricht.
Dit zijn allemaal systemen met een of andere vorm van terugkoppeling. Bij al dit soort teruggekoppelde systemen vergelijk iemand of iets steeds of de gemeten waarde al gelijk is aan de gewenste waarde (via een comparator; een vergelijkend orgaan of element).
Eerste en tweede orde systemen
De dynamica van niet-teruggekoppelde systemen is heel anders dan van de teruggekoppelde systemen.
Er zijn eerste, tweede en (nog) hogere orde systemen. De orde van het systeem hangt af van het aantal tijdconstanten er in de voorwaartse loop, in het besturende systeem (B.S.), zitten. Dit verschil is zeer dominant in het dynamische gedrag van het gehele (teruggekoppelde) systeem. We zullen hieronder laten zien wat de dynamica van dit soort 1e, 2e of hogere orde systemen is. Bij een eerste orde besturende systeem (B.S.) gaat de output vrij rustig naar de ingestelde waarde; bij een tweede orde besturende systeem (B.S.) gaat de output meestal slingerend naar de ingestelde waarde. Zie de twee verschillende applets elders op deze pagina.
Als u in de eerste onderstaande applet de input op een bepaalde waarde zet ('target'), dan ziet u de output rondom die waarde tot stilstand komen c.q. stabiliseren. Omdat zowel het eerste systeem als het tweede systeem teruggekoppeld is. D.w.z. beide systemen kunnen net zo lang doorgaan tot de gemeten waarde gelijk is aan de gewenste waarde. Dan stoppen beiden. Als u hetzelfde doet in het tweede teruggekoppelde systeem ziet u soortgelijk gedrag. Alleen dan kunnen er in bepaalde gevallen overshuut reacties plaatsvinden. Bij teruggekoppelde eerste orde systemen kan dat niet.
Interactieve applet
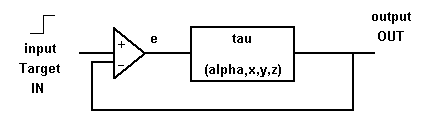
Figuur 3. U ziet hier een conceptueel schema van een teruggekoppeld eerste orde systeem, incl. een interactieve simulatie ervan. Het dynamisch gedrag van dit systeem, in de tijd, kunt u hieronder zelf uitproberen. (We noemen dit in de onderwijskunde een micro-wereld.) Hierdoor/hiermee kun je zien hoe feedback werkt. Klik op 'start' en laat de tijd laat lopen. Als je een bepaalde waarde als 'target' ('IN') kiest dan zal de output van dit systeem ('OUT') na verloop van tijd op de waarde van dat target uitkomen.
Interactieve applet

Figuur 4. U ziet hier een conceptueel schema van een teruggekoppeld tweede orde systeem, incl. een interactieve simulatie ervan. Het dynamisch gedrag van dit systeem, in de tijd, kunt u hieronder zelf uitproberen. (We noemen dit in de onderwijskunde een micro-wereld.) Hierdoor/hiermee kun je zien hoe feedback werkt. Klik op 'start' en laat de tijd laat lopen. Als je een bepaalde waarde als 'target' ('IN') kiest dan zal de output van dit systeem ('OUT') na verloop van tijd op de waarde van dat target uitkomen. Kenmerk bij tweede orde processen (B.S.) is de overshuut reactie van de output.
Het systeem-denken leidt tot een beter wereldbeeld, een wereldbeeld dat beheerst wordt de essentie van een fenomeen te kunnen scheiden van de technische kant (ofwel de dynamische kant). Kans en keuze en de invloed van de omgeving zijn essentieel voor het begrijpen van verschijnselen (Kramer en De Smit, blz. 5). Door het begrijpen van systemen kom je tegelijkertijd ook los van het deterministische kant van een systeem. De output-georienteerde wijze van kijken zal tijdens je studie vruchtbaar blijken te zijn. Zorg altijd dat je dit soort - dynamisch - gedrag kunt herkennen. Dat geeft je een voorsprong op onderzoekers die alleen maar fenomenologisch naar dingen kijken.
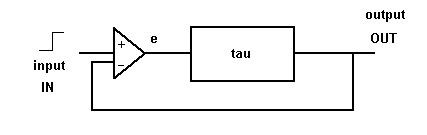
Figuur 5. Een interactieve animatie annex simulatie. Hier kun je ook zien hoe feedback werkt. (We noemen dit in de onderwijskunde een micro-wereld.) Klik op 'start' en laat de tijd laat lopen. Als je een 'target' (IN) kiest dan zal de output na verloop van tijd op dat target uitkomen (OUT).
Online example: een fundamenteel regelsysteem met target(s) instellling (2003)
Een voorbeeld van een (gewoon) deterministisch systeem, dat in de praktijk toch ingewikkeld is dan de meeste waarnemers denken, is de glucosehuishouding van de mens. De hoeveelheid glucose in het bloed (de waarde daarvan wordt de bloedspiegel genoemd) hangt direct af van de regulatie van de insuline (en omgekeerd). In een gezonde huishouding is glucose direct gekoppeld aan insuline en is de homeostase (het constant houden) van de insuline zowel als de glucose geregeld. Door op onregelmatige tijden te eten (at random) kan dit systeem in de verste verte niet meer op een deterministische manier begrepen worden. Daardoor is dit systeem dan ook stochastisch. Als insuline een medisch probleem is geworden, dan kan de glucose (ook) niet meer goed geregeld worden. Insuline moet dan kunstmatig, op het juist moment en in de juiste hoeveelheid worden aangevuld.
In vroegere tijden was er het machine-denken. Van feedback-loops had men daarbij nog geen benul. De beperkingen daarvan waren evident. (Zie elders.) Essentiele eigenschappen van dingen konden niet afgeleid worden uit (onder)delen of interacties tussen (onder)delen van systemen. Persoonlijkheid en intelligentie van de mens kon niet worden geplaatst. Bepaald intelligent gedrag ook niet. Daarna kwam het systeem-denken op gang, feedback-loops werden ontdekt en het (permanent/voortdurend/automatisch) (kunnen) vergelijken van grootheden werd veel meer en beter begrepen.
Het systeem-denken heeft zijn wortels in de biologie, de psychologie, de technologie, de methodologie, de communicatietheorie en de - lelijk woord - cybernetica.
In de psychologie (blz. 7-8) werd vroeger gedrag wel eens verklaart met behulp van een mechanisch stimulus-respons-model (en eenvoudige oorzaak-en-gevolg-relaties). Voor veel aspecten in de levende natuur blijken dit soort modellen zinloos en fout. De gestaltpsychologie kwam daarna op. Minuchin, 1973, Hendrickx, 1981, en Ashby, 19xx, legde daarna het theoretisch fundament in de systeemtheorie. De successen begonnen in de gezinstherapie-hoek. Daarna werd daarmee veel duidelijk op het terrein van de management- en bedrijfskundige problematiek (denk aan de quality control systems van Juran). Ook op het niveau van de samenleving en maatschappelijke problemen bleek het systeemdenken zin te hebben; en niet te vergeten op het gebied van de macro-economie, bij leren en leertheorieen, de cognitieve psychologie en aangaande groepsdynamica. Maar we moeten - anno 2003 - ook weer niet al te veel doorslaan en met beide benen op de grond blijven. Systeemdenken is wel altijd een eerste of tweede stap, maar niet (nooit?) de laatste stap. Vaak spelen er aan de ene (uiterste) kant emoties en/of aan de andere (uiterste) kant nog heel vulgair materialistische zaken een dominante of verklarende rol.
Referenties
Kramer, N.J.T.A. & J. De Smit (1991). Systeemdenken. Stenfert Kroese. Leiden/Antwerpen http://projects.edte.utwente.nl/pi/Sheets/SysBen/index.html
Min, R., H. Vos, P. Kommers en van Dijkum (19xx). Over leren, plannen en jezelf testen: http://home.tiscali.nl/schopmanlanden.nl/Papers/Learning.htm
Min, R. (19xx). Over regelen, besturen en beheren:
http://home.tiscali.nl/schopmanlanden.nl/Papers/Designing.htm
Robertson, R.J. & W.T. Powers (1990).
Introduction to Modern Psychology; the Control Theory View.
Op- en aanmerkingen op deze eerste versie zijn altijd welkom.
Enschede, June, 5, 2003. versie 1.02










