jan. 13, 2003
Technology + Simulation
Reminder
At this moment you have had: an introduction and a problem
Other remarks:
- Homework: thinking about simulations and learning environments;
- Homework: Looking to the article about Simulation and Learning;
- Homework: Looking to the 27 parts for your simulation;
- Today: Some important aspects of models;
- Homework this week: looking and reading parts of my book;
- Deadline task 1, writing a paper about simulation: March 17, 2003;
- Deadline task 2, develop a applet as object in an educational website: March 3, 2003;
About models
From a concept to a mathematical model
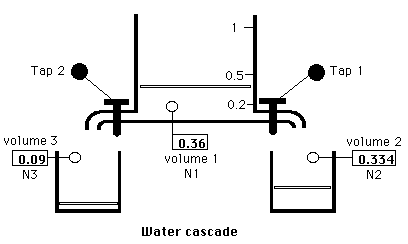
Conceptual representation of a mathematical model ('conceptual model') (concrete) (1)
Conceptual representation of a mathematical model ('conceptual model') (concrete) (2)
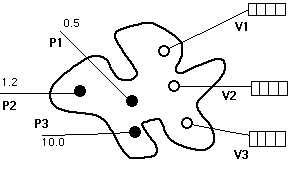
Conceptual representation of a mathematical model ('conceptual model') (abstract)
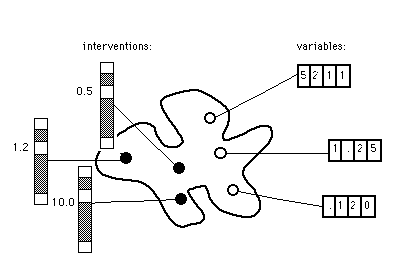
The same: with scrollbars.
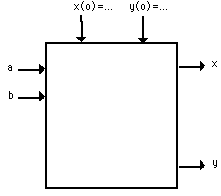
Black box of a model
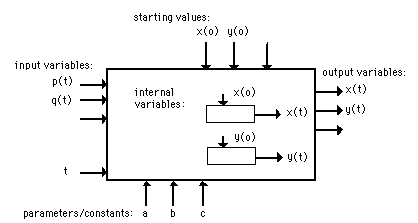
Block scheme or black box model; variables (a), starting values (b), parameters and constants
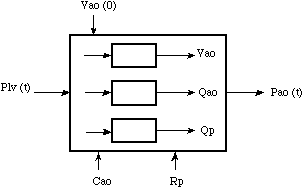
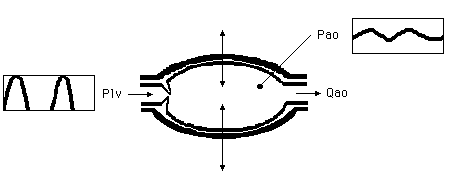
Block scheme of the pressure changes in black box model of the aorta.
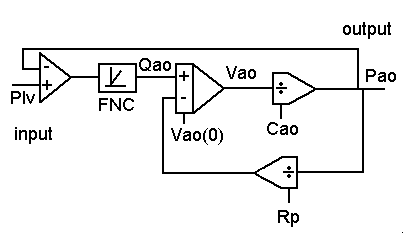
Analogue scheme of the pressure changes in the aorta. In such schemes you can see the 'cause' in relation to the 'result'.
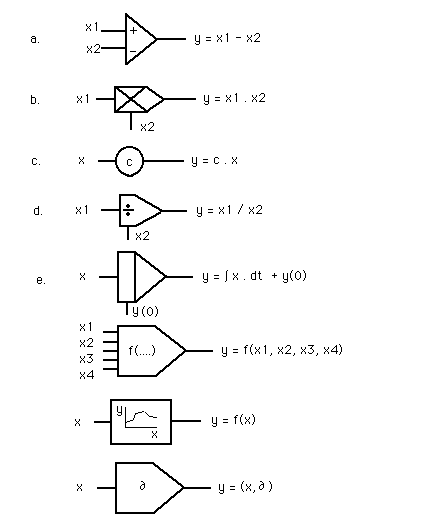
Analogue components (e-Book, Min, 1997-2003).
Repeat
t = t + dt;
Plv = Plvmax*Math.sin(2 * 3.14 * f * t);
if (Plv < 0.0) { Plv = 0.0}
Qao = 33 * (Plv - Pao);
if (Plv < Pao) {Qao = 0.0}
Pao = Vao / Cao;
dVaodt = Qao - Pao / RP;
Vao = Vao + dVaodt * dt;
Until t > Tmax
Java way of notation.
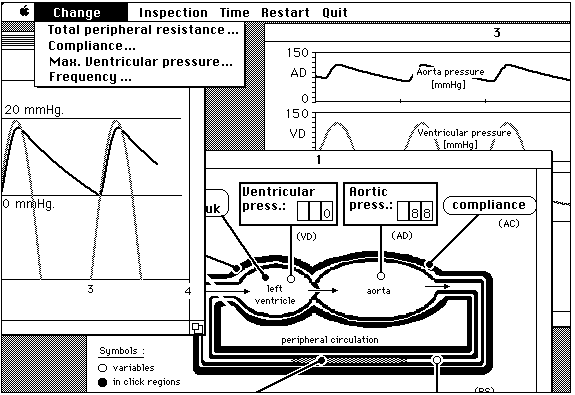
The complete computer simulation program AORTA. One window with the conceptual model and 'inclick regions' and two 'output windows' with different graphical presentations of the model variables.
click here
The complete computer simulation program AORTA, version Rinske Stelwegen, 2001.
click here
The complete computer simulation program AORTA, versie R. Min, met DHTML, 2002.
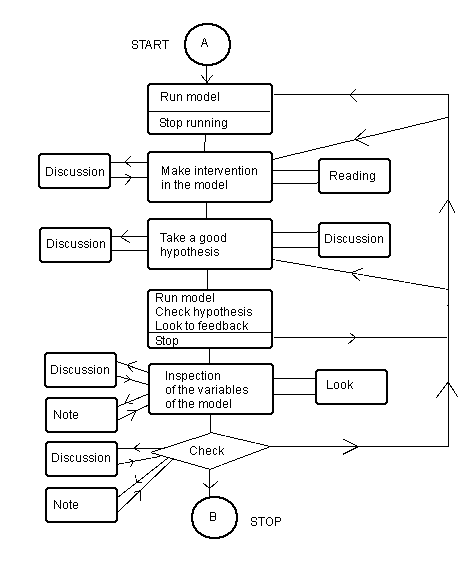
Learning model. There are six learning models in learning with simulations.
Test
Make a black box model of this (with all the variables and all the parameters !)
Repeat
t = t + dt;
Plv = Plvmax*Math.sin(2 * 3.14 * f * t);
if (Plv < 0.0) { Plv = 0.0}
Qao = 33 * (Plv - Pao);
if (Plv < Pao) {Qao = 0.0}
Pao = Vao / Cao;
dVaodt = Qao - Pao / RP;
Vao = Vao + dVaodt * dt;
Until t > Tmax
Repeat
t = t + dt;
UB = Ucc*R2/(R1+R2);
URE = URE + ((UB - 0.7) - URE)*0.03;
IR2 = UB/R2;
IR1 = (Ucc - UB)/R1;
IE0 = URE/RE;
IC0 = IE0;
IB0 = 0.0;
UC = Ucc - IC0*RC;
UCE = UC - URE;
ui = 100*A * Math.sin(2* 3.1418 * f * t);
if (ui > A) {ui = A;}
if (ui < -A) {ui = -A;}
ui1 = ui1 + (ui - ui1)*0.2;
i1 = ui/R1;
i2 = ui/R2;
ib = i1-i2;
ic = -beta*ib;
uo = -40*IC0*RC*ui1;
Uuit = UC + uo;
Uin = UB + 15.0*ui;
Error = Ucc - (IC0*RC + UCE + URE);
Controle = R1*IR1+R2*IR2;
Until t > Tmax
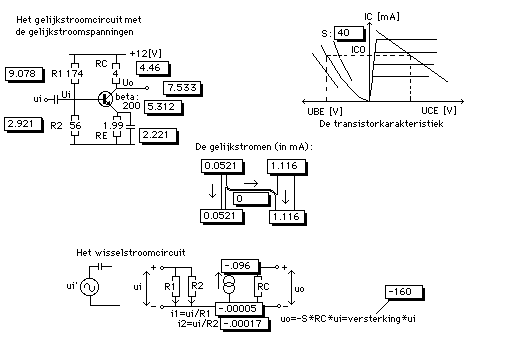
The conceptual scheme; left-up.
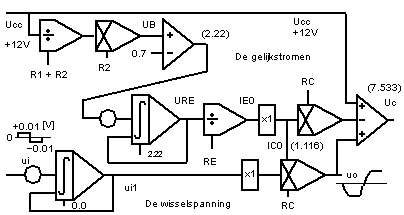
The analogue way of notation; the analogue scheme.
Enschede, jan. 13, 2003













