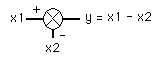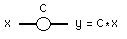Wat is een analoog schema?

Een regelsysteem is eigenlijk altijd een wiskundig model. Als je een regelsysteem wilt simuleren, zul je het regelsysteem altijd in gewone wiskundige formules moeten omvormen. Bij het beschrijven van een regelsysteem - in wiskundige formules - blijken er altijd een of meer integraalvergelijkingen in de formules te zitten. Dergelijke integraalvergelijkingen zijn niet zo maar uit te rekenen; je hebt er een analoog schema voor nodig. Analoge schema's zijn dus van belang als je een simulatie wilt maken en zijn voor een deel ook nog van belang om op een iets andere manier naar regelsystemen te kijken dan gebruikelijk. Daarom hier een korte introductie op analoge schema's.

Een analoog schema

In dit soort schema's van processen, systemen of modellen worden in principe (altijd) gestandaardiseerde symbolen gebruikt: driehoeken, blokken en/of circels en combinaties daarvan. Maar sommige symblolen hebben twee of drie notatiewijzen. Een integrator is symbolisch als in figuur 1b voor te stellen. Een opteller zie je in figuur 1a. Als dit soort symbolen voor integreren of optellen worden gebruikt, dan spreken we van een analogon. Vandaar het woord analoog schema. We zullen in de voorbeeld van de waterbak twee symbolen de revu laten passeren: het symbool van de integrator zelf en het symbool voor optellen, aftrekken, vermenigvuldigen en delen.

Figuur 1. De twee belangrijkste symbolen voor analoge schema's:
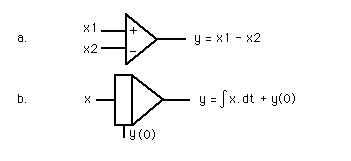
a. Het symbool van een 'opteller'. De output is y. De opteller 'telt' de ingangssignalen, x1 en x2, 'bij elkaar op' of 'trekt' twee ingangssignalen van elkaar 'af'.
b. Het symbool van een 'integrator'. De output is y. En y is 'de integraal van de input'. De input is hier x. Het integreren begint altijd op het niveau van de startwaarde y(0).
c. Het symbool van een 'vermenigvuldiger'. De output is x1 * x2.
d. Het symbool van een 'deler'. De output is x1/x2.

Een 'opteller' kan ingangswaarden of ingangssignalen bij elkaar optellen; of trekt ze van elkaar af. In het laatste geval dient er een 'min'-teken aan de ingang te staan. Er bestaan ook symbolen voor vermenigvuldigen en delen. Alleen de 'opteller', die ook 'negatief' of negatieve signalen kan optellen is - hier - voor ons relevant. (Zie figuur 1a.) De input c.q. het ingangssignaal bij een symbool als deze symbolen, is bijna altijd een variabele en bijna altijd van elders afkomstig.

In de regeltechniek wordt voor een opteller of aftrekker ook vaak en circel met een maalteken erdoor gebruikt. Zie hiernaast of figuur xxx en elders.
Deze circel niet verwarren met een ander symbool (met een cirkel) dat een inputsignaal kan vermenigvuldigen met een constante waarde. Zie hiernaast of figuur xxx en elders.

Een 'integrator' telt steeds de waarde van de ingang (x) op bij de reeds aanwezige waarde (y). Het ingangswaarde kan positief of negatief zijn. Positief wil zeggen toenemende accumulatie; negatief wil zeggen minder of het omgekeerde van accumulatie ('negatieve accumulatie'). De formule die naast figuur 1b staat, spreekt voor zich.

Figuur 2. Het complete analoge schema van de waterbak (variant a en b):
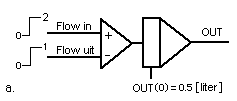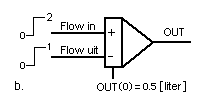
a. De integrator heeft aan de inputkant een losse, aparte opteller.
b. De integrator heeft geen aparte opteller maar zelf twee 'ingangen'.
c. De integrator heeft xxx met twee 'ingangen'.
De startwaarde van de integrator is OUT(0) en hier steeds 0.5 [liter]

Het analoog schema van xxxx ziet er uit als in figuur xx is afgebeeld.

Figuur 3. Meer complete analoge schema's:
a. Met een zuivere terugkoppeling; d.w.z. nergens een constante. OUT is op de lange duur gelijk aan 2 en begint bij 0.5.
b. Met een terugkoppeling en een constante (c) die niet 1 is (zoals bij hierboven bij a). OUT is op de lange duur niet gelijk aan 2, maar hangt helemaal van de waarde van c af; en begint bij 0.5
c. Met een terugkoppeling en een constante (tau) die niet 1 is. OUT is op de lange duur niet gelijk aan 2, maar hangt van de waarde van tau af. OUT begint bij 0.5.
De startwaarde van de integrator is in alle drie de voorbeelden steeds 0.5 [liter]

Figuur 4. Meer voorbeelden van complexe analoge schema's:
a. Met twee terugkoppelingen en een vermenigvuldiger in de teruggekoppelde weg en de voorwaardse weg.
b. Met twee achter elkaar geschakelde eerste orde processen en een overall feedback-lus met een klein procesje erin.
c. Met een niet-lineaire overgangs-blok erin. De ingang is een sinusvormig ingangssignaal. (Zie elders; bijvoorbeeld bij de zonneboiler.)
De startwaarde van de integrator is hier ook steeds 0.5 [liter]

Je hebt nu kort kenisgemaakt regelsystemen, wiskundig modellen en analoge schema's. Modellen bevaten altijd wel een integraalvergelijking en die zijn daarom niet zo maar uit te rekenen. Je hebt dan een analoog schema voor nodig. Analoge schema's zijn dus van belang als je een simulatie wilt maken.

Dit interactieve product over 'integratoren' en 'analoge schema's' is in 2008 gemaakt voor ROC Hengelo. Er zijn meerdere e-lessen, elders, m.n. over 'eerste orde en tweede orde regelsystemen'. De docent in wiens opdracht dit gemaakt is, had maar een klein budget tot zijn beschikking. Digitale producten als dit, met interactieve applets, kunnen eindeloos uitgebreid worden. Bijvoorbeeld met interactieve intelligente objecten met oefenfaciliteit, geluid, een mensenlijke stem of video. (Zie elders.)