AORTA, version JavaTHESIS 3.3x.
Atherosclerosis in relation to compliance and peripheral resistance
by J. Sikken, B. Reimerink & R. Min, sept. 1997
Here appears a button for the simulator of AORTA with a young, normal male person (an 'applet'). Downloading the applet costs 10 to 30 seconds on the WEB. It depends on your system and the moment of the day. The simulator itselfs will comes automatically if you press the button. This program is an applet, writen in Java. More information about the model and the eductional aim is showed at the end of this page.
Hierboven ziet u de interactieve model-driven java-applet....
Information about the model and users instruction
As an example of the various ways of
representation of a simple model from the medical section are shown here.
The model will be functionally described without really going into detail.
For a description of the educational possibilities of this model the reader
is referred to the description of the computer simulation program AORTA by Min and
Struyker Boudier elsewere.
Educational aim
In early phase of their studies medical students can familiarize
themselves with some basic concepts from hemodynamics and some aspects
of arteriosclerosis. In using this program an answer is given to
questions like
'What happens if the total peripheral resistance of the circulation is
increased?'
The opposite can also be an educational goal, namely the question as to what
is the cause of the deviating picture of the diastolic pressure in the aorta.
'Can the cause of a decreased diastolic pressure in the aorta be a decreased
compliance of the aorta? Yes or no?'
Students learn to handle notions like compliance and total peripheral resistance
and changes there in. Students are supposed to be able to formulate questions
and/or hypotheses and to verify these hypotheses with the help of this simulation
program.
Within the framework of a course about arteriosclerosis, case studies has been
developed about the hardening of the wall of the aorta and the increased total
resistance of the peripheral circulation. In this case study the students
themselves have to recognize that the mean peripheral stream has changed and they
have to try to restore it by adapting the pressure of the ventricle. The program
is intended to teach the students how to deal with basal hemodynamic relations
such as between pressure, compliance and volume and those between stream, resistance
and pressure and to determine the consequences of interventions in hemodynamic
variables.
Introduction in the model
As an example of the various ways of
representation of a simple model from the medical section are shown here.
The model will be functionally described without really going into detail.
For a description of the educational possibilities of this model the reader
is referred to the description of the computer simulation program AORTA by Min and
Struyker Boudier elsewere.
Educational aim
In early phase of their studies medical students can familiarize
themselves with some basic concepts from hemodynamics and some aspects
of arteriosclerosis. In using this program an answer is given to
questions like
'What happens if the total peripheral resistance of the circulation is
increased?'
The opposite can also be an educational goal, namely the question as to what
is the cause of the deviating picture of the diastolic pressure in the aorta.
'Can the cause of a decreased diastolic pressure in the aorta be a decreased
compliance of the aorta? Yes or no?'
Students learn to handle notions like compliance and total peripheral resistance
and changes there in. Students are supposed to be able to formulate questions
and/or hypotheses and to verify these hypotheses with the help of this simulation
program.
Within the framework of a course about arteriosclerosis, case studies has been
developed about the hardening of the wall of the aorta and the increased total
resistance of the peripheral circulation. In this case study the students
themselves have to recognize that the mean peripheral stream has changed and they
have to try to restore it by adapting the pressure of the ventricle. The program
is intended to teach the students how to deal with basal hemodynamic relations
such as between pressure, compliance and volume and those between stream, resistance
and pressure and to determine the consequences of interventions in hemodynamic
variables.
Conceptual model (visual and textual)
The conceptual model of a beating aorta of a human being looks like the drawing
in figure xxx. The aorta is the great artery which springs from the left ventricle
in the heart. The heart pumps (with a certain pressure, here Plv) a quantity of
blood through the human body with each heart beat (Qao) attended by a change in
pressure in the aorta. The aorta itself is elastic. The quantity which plays a
role in the elasticity of the aorta is compliance (Cao). There is a connection
between the form of the changes in pressure in the aorta and compliance.
Furthermore there is a connection between the blood pressure in the aorta (Pao),
the quantity of blood which flows through the aorta (Qao) and the resistance
offered by the body (the peripheral resistance, Rp). The interesting variable
to be measured externally, 'the pulse pressure', is practically equal to the
pressure of the aorta. This pressure varies considerably and is very
characteristic.
Block scheme of the model
An inventory of this model, textual represented above, gives the following results:
- ventricle pressure (Plv) (in mmHg) (an input variables)
- blood pressure in the aorta (Pao) (in mmHg) (an output variables)
- blood volume (Vao) (in ml) (an state variable)
- blood flow per time unit (flow) at the entrance of the aorta (Qao)
(an state variable)
- blood flow per time unit (flow) at the exit of the aorta (which is equal
to the total blood
- flow through the body: the peripheral flow) (Qp) (an state variable)
- maximum (left) ventricle pressure (Plvmax) (in mmHg) (a model parameter)
- heart frequency f in 1/sec (a model parameter)
- compliance of the aorta (Cao) (a model parameter)
- peripheral resistance (Rp) (a model parameter)
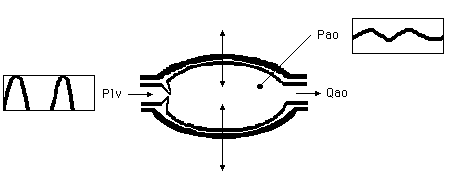
The conceptual scheme of AORTA
Integral equation of the model
One can speak of one output variable, one input variable, three state
variables and four (model)parameters which can serve as intervention possibilities.
The model in the form of a system of integral equations
Plv = Plvmax * sin (2 * 3,14 * f * t); ( if Plv < 0 then Plv = 0.0 !)
Qao = 33 * (Plv - Pao); ( if Plv < Pao then Qao = 0.0 !)
Qp = Pao / Rp
Vao = int { (Qao - Qp) . dt } + Vao(0)
Pao = Vao / Cao
For the sake of convenience, the input variable is approached by half a sinus.
Analogue notation
Of this model a complete analogue scheme can be made. The non-linear function
of conveyance is represented by a (non-linear) function block.
Java notation
The model in the Java notation way looks as follows, apart from details:
t = 0.0;
Plv = 120.0; <--- model variables
Qao = ....;
Pao = 80.0;
Vao = 80.0;
Rp = 1.25; <--- model parameters
Cao = 1.1;
f = 1.0;
PlvMax = 120.0;
Tmax = 4.0; <--- program constants
dt = 0.02;
inside the repeat or while-loop the model (Until t > Tmax):
tijd = tijd + dt;
Plv = PlvMax * Math.sin (2.0 * 3.14 * f * tijd);
if (Plv < 0.0) Plv = 0.0;
Qao = 33.0 * (Plv - Pao);
if ((Plv-Pao) < 0.0) Qao = 0.0;
Vao = Vao + (Qao - Qp) * dt;
Qp = Pao / Rp;
Pao = Vao / Cao;
The integration statements (here only one) are best all taken at the end, so
that it is certain that the old and new values of the variables will not
become mixed up.
Results
The blood pressure can be seen at specific and characteristic
values of peripheral resistance (Rp) and compliance (Cao). In one case built
in the program it can be seen that the pressure during the systole has become
high and in a second case the medical student can see that the pressure during
the diastole is low. A first year medical student has to be able to diagnose in
the first case of these 'clinical pictures' that something is wrong with the
peripheral resistance and in the second case with the compliance. After that
an experiment has to show if a change (upwards or downwards) of the peripheral
resistance of compliance brings any improvement. If the 'patient' only becomes
worse the students' hypothesis was wrong.
Some examples (in Dutch): een 'opdracht', een 'casus' & een opdracht voor een 'wetenschappelijk experiment'
Print deze opdrachten uit op papier en gebruik deze papieren opdrachten naast de computer; naast de browser
A. Een voorbeeld van een 'opdracht'
Opdracht 'Echte' hoge bloeddruk (TPW en Vdmax)
1. Start of herstart het model of het programma
2. Laat het model precies een hartslag maken en stop dan
3. Verhoog de totale perifere weerstand TPW van 1.25 tot 1.8 eenheden
4. Beantwoord, alvorens verder te gaan, eerst de volgende vragen:
De aortadruk wordt in zijn totaliteit…hoger/lager*)
De bovendruk wordt:........................................................................hoger/lager*)
De onderdruk wordt:.........................................................................hoger/lager*)
Dit noemen wij de hypothese! Deze hypothese kunt u gaan toetsen met het programma
5. Laat het model nog één hartslag maken en stop dan
6. Verhoog vervolgens ook de ventrikeldruk VD door de maximale ventrikeldruk (Vdmax) te verhogen van 1.25 tot 1.5 eenheden
7. Beantwoord, alvorens verder te gaan, eerst de volgende vragen:
De aortadruk wordt in zijn totaliteit........................hoger/lager*)
De bovendruk wordt:........................................................................hoger/lager*)
De onderdruk wordt:.........................................................................hoger/lager*)
Dit noemen wij de hypothese! Ook deze hypothese kunt u gaan toetsen.
8. Laat het model vervolgens nog twee hartslagen maken. Stop het model na de vierde hartslag, juist voordat de maximale rekentijd is bereikt.
9. Hoe groot is de druk in de aorta, de aortadruk AD, minimaal en maximaal?
Minimale aortadruk AD:................................................mmHg
Maximale aortadruk AD:................................................mmHg
Komt uw veronderstelling (hypothese) overeen met de werkelijkheid .. ja/nee*)
10. De relatie tussen het verhogen van de (maximale) ventrikeldruk (Vdmax) tezamen met het verhogen van de totale perifere weerstand (TPW) is dat de bovendruk en de onderdruk wordt:.................................................................hoger/lager*)
P.S: als iets onverhoopt niet direct lukt, kunt u altijd het model of het programma herstarten.
*) omcirkel datgene wat van toepassing is.
B. Een voorbeeld van een 'casus'
1. Start of herstart casus 3
2. Laat het model ongeveer twee hartslagen maken en stop dan
3. Welke afwijking ziet u ten opzichte van het normale beeld. **)
de bovendruk: hoger/lager gelijk gebleven*)
de onderdruk: hoger/lager gelijk gebleven*)
4. Welke parameter (of parameters) denkt u dat hiervoor verantwoordelijk is (zijn)?
Totale perifere weerstand................................................ja/nee*)
compliantie.........................................................................................ja/nee*)
slagfrequentie..................................................................................ja/nee*)
ventrikeldruk........................................................................................ja/nee*)
5. Deze parameter is:..........................................................te groot/te klein*)
Dit is uw hypothese.
6. Tracht nu het normale beeld te herstellen door bovengenoemde parameter ten goede te veranderen. Als het niet direct lukt, is dat geen probleem. U mag ook in enkele stappen dat doel bereiken.
7. Mijn hypothese over de verantwoordelijke parameter was:..........................goed/ongeveer goed/fout*)
8. Mijn hypothese over te groot of te klein was:........................................................goed/ongeveer goed/fout*)
*) Omcirkel datgene wat u van toepassing vindt
**) Bij deze casus zijn twee parameters veranderd. Let op
C. Een voorbeeld van een opdracht voor 'een wetenschappelijk experiment'
(hier: en dosis-respons-curve onderzoeken en opstellen)
1. Laat model steeds lopen (steeds herstarten)
2. Stop op de eerste dag steeds (bij het eerste streepje)
3. Maak deze patient nu 'kunstmatig' ziek door RM (renale massa) van 1 naar 0.5 te verkleinen
4. Laat het model vervolgens steeds twee dagen “uitzieken”. De bloeddruk is nu licht verhoogd (ongeveer 11 mmHg)
5. Geef na drie dagen in steeds wisselende dosis het geneesmiddel, “een sympathicoliticum”
Geneesmiddel bloeddruk (AP) (OP PAPIER INVULLEN SVP)
0.0 ............................
0.3 ............................
0.6 ............................
0.8 ............................
1.0 ............................
6. Noteer steeds op de vijfde dag, als de maximale rekentijd is bereikt, hoe groot de bloeddruk is geworden
(een sympathicoliticum is een bloeddruk verlagend geneesmiddel bij hoge bloeddruk patienten)
7. Teken de gevonden waarden in een grafiek op het bijgeleverde millimeterpapier
8. Is dit middel inderdaad bloeddruk verlagend?..........................ja/nee*)
*) invullend wat verlangd wordt

