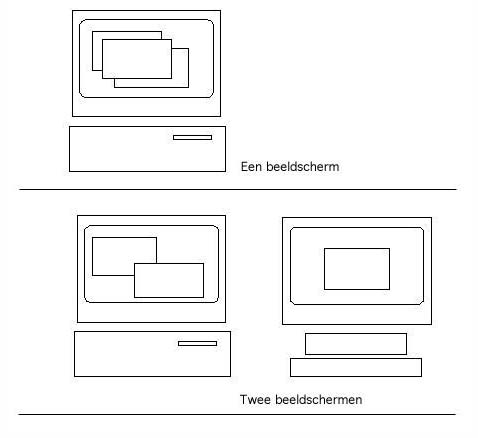
Figuur 1. De twee beeldscherm-condities

Door: U.A. Groenewoud en J. ter Burg (studenten), m.m.v. W. Akkermans (methodoloog) en R. Min (supervisor); Faculteit Toegepaste Onderwijskunde, Universiteit Twente, Enschede NL.
Dit artikel is geschreven in het kader van het vak 'onderzoekspracticum'. Het is officieel gepubliceerd in de proceedings van dat vak; Editors: W. v.d. Linden, S. Oosterloo en H. Vos, Universiteit Twente, Enschede NL (1996).
Key-words: leermodel; kwalitatieve leermodellen, kwantitatieve leermodellen, empirisch onderzoek.
Simulatie kan worden gedefinieerd als een natuurgetrouwe nabootsing van werkelijke situaties (Digital Equipment, 1984). De werkelijke situaties worden weergegeven in een model met een aantal parameters die gemanipuleerd kunnen worden door de leerlingen. De leerlingen kunnen op deze manier inzicht verkrijgen in de processen uit de werkelijkheid en/of intellectuele vaardigheden die hieraan ten grondslag liggen ontwikkelen (Dirkzwager, 1987). Moore en Thomas (1983) constateren in hun werk dat computersimulaties dezelfde cognitieve en affectieve doelen dienen als laboratorium-werk, zoals 'learning skills and techniques, aiding pupils' understanding of the subject matter and facilitating concept formation, helping the pupils to hypothesize and develop an understanding of the scientific method [and] motivating and stimulating interest in the study of science'. De belangrijkste bedoeling van onderwijskundige computersimulaties is om studenten te helpen bij het construeren van mentale modellen van dynamische processen (Min, 1994).
In het algemeen is er in een simulatieprogramma sprake van veel verschillende soorten informatie, zoals informatie over het model, over de input-variabelen en de (bijbehorende) outputgegevens. Om al deze gegevens op een overzichtelijke manier voor de gebruiker te kunnen presenteren bestaat een simulatieprogramma vaak uit verschillende windows. Op deze manier kunnen de verschillende soorten informatie (het model, de input, de output, etc.) duidelijk voor de leerling van elkaar gescheiden worden (o.a. Rivlin e.a., 1990) en het effectieve oppervlak van één beeldscherm kan hiermee vergroot worden (Min, 1996). Leerlingen kunnen tussen de windows switchen; 'Het naar voren halen van een window door er op te klikken is de meest handige manier om het effectieve oppervlak van een beeldscherm te vergroten. Het voorliggende window verdwijnt dan naar de achtergrond. Het achterliggende window komt naar voren. Het voorliggende window is nu het actieve window maar in de andere windows gaan processen soms gewoon door' (Min, 1996). Als er meerdere soorten programma's geladen zijn noemt Min de verschillende soorten simultane processen 'waarbij er allerlei soorten visuele en auditieve informatie naast elkaar, door elkaar en over elkaar heen buitelen' parallelle processen. Situaties waarin alle windows in één oogopslag zijn te overzien definieert Min als eerste orde parallellisme, situaties waarin de windows zich op over elkaar liggende dragers bevinden definieert hij als tweede orde parallellisme.
Volgens Min (1994) houden leerlingen in werk-, doe- en leeromgevingen ervan om alles te kunnen (blijven) overzien, eerste orde parallellisme heeft dan de voorkeur, omdat het effectieve beeldscherm-oppervlak dan groot is. Het probleem bij eerste orde parallellisme is echter, volgens Min, dat de ontwerper uiteindelijk toch behoefte heeft aan een groter beeldscherm-oppervlak dan de standaard- PC. 'De ruimte op de standaardcomputer is [voor simulaties] gewoon erg beperkt. De monitor - zo is uit ons onderzoek gebleken - is op een bepaalde manier een heel gebrekkig en onhandig onderdeel van de hedendaagse PC'.
In het voorliggende onderzoek is gekeken of de mate van parallellisme van invloed is op de werksnelheid en of de proefpersonen eerste orde parallellisme inderdaad prefereren boven tweede orde parallellisme. De eerste onderzoeksvraag is onderzocht aan de hand van gegevens uit een logfile waaruit duidelijk wordt hoelang de proefpersonen bezig zijn geweest met het uitvoeren van een taak met behulp van het simulatieprogramma CARDIO. Naast de tijd die de proefpersonen nodig hadden om de antwoorden te geven, werd ook een andere, volgens D. E. Egan (1988), zeer belangrijke variabele 'aantal fouten' geregistreerd. Er werd verwacht dat de mate van parallellisme geen invloed heeft op de werksnelheid, omdat de meeste computergebruikers gewend zijn aan meerdere windows op Žen beeldscherm en snel tussen de overlappende windows kunnen switchen. De tweede onderzoeksvraag is onderzocht met behulp van een vragenlijst. Deze vragenlijst is aan studenten voorgelegd nadat zij gewerkt hadden in beide beeldscherm-condities: in de ene conditie werkten zij met het simulatieprogramma CARDIO waarbij er bij de beeldschermvormgeving sprake was van eerste orde parallellisme en in de tweede conditie werkten zij met hetzelfde programma, maar was het beeldschermoppervlak dusdanig kleiner dat er sprake was van tweede orde parallellisme.

Er werd verwacht dat de proefpersonen een voorkeur hadden voor het werken met twee beeldschermen, dus dat de proefpersonen een voorkeur hadden voor eerste orde parallellisme.
Materialen
Het multi-windowing-simulatieprogramma, waarmee in dit onderzoek gewerkt is, is CARDIO, versie 5.0x (1996). Dit simulatieprogramma geeft een model van het cardiovasculair systeem en zijn controle mechanismen. In dit onderzoek is gebruikt gemaakt van de mogelijkheid om de bloeddruk te verlagen door middel van het 'toedienen' van een door de gebruiker te bepalen dosis van een medicijn.
Ten behoeve van dit onderzoek is een onderzoeksinstrument ontwikkeld. Dit onderzoeksinstrument is een Hypercardstack die naast het simulatieprogramma CARDIO liep. Beide programma's liepen op een Macintosh-II. De Hypercardstack was opgedeeld in een korte instructie en het experiment. De instructie bestond uit een oefening die op dezelfde manier was opgebouwd als het experiment. Zij is aan het onderzoeksprogramma toegevoegd om bij de proefpersonen het programma en het experiment te introduceren en om iedereen de mogelijkheid te geven om te oefenen met de computer en zo vertrouwd te raken met zijn/haar conditie en het experiment. Het experiment bestond uit een taak waarbij de proefpersonen een bepaalde dosis van een medicijn, beide aangegeven door de Hypercardstack, moesten invoeren in het simulatieprogramma CARDIO. Na het lopen van het model in de tijd moesten de proefpersonen vervolgens de outputgegevens van het simulatieprogramma invoeren in de Hypercardstack.
Naast de instructie en het experiment bevatte het onderzoeksinstrument een voor de proefpersonen onzichtbaar onderdeel, een logfile. In deze logfile werd de tijd die de verschillende proefpersonen per onderdeel nodig hadden bijgehouden. Ook andere belangrijke variabelen, zoals het aantal keren dat de oefening doorlopen werd en het aantal fouten dat gemaakt werd, werd geregistreerd. Wanneer een proefpersoon een verkeerde waarde in de tabel invulde werd dit geregistreerd als een fout.
De vragenlijst bestond uit 8 vijf-punts zowel positief als negatief gestelde vragen waarop de proefpersonen o.a. konden aangeven of ze het werken met twee beeldschermen ten opzichte van het werken met één beeldscherm vermoeiender dan wel niet vermoeiender vonden. Zij konden hun mening aangeven door één van de getallen 1 tot 5 te omcirkelen, waarbij 1 betekende dat zij vonden dat het werken met twee beeldschermen niet vermoeiender was ten opzichte van het werken met één beeldscherm en 5 betekende dat zij dit wel vermoeiender vonden. De andere vragen gingen over het verschil in moeilijkheid, handigheid, overzichtelijkheid, omslachtigheid en leuk zijn tussen de twee condities. Ook werd de proefpersonen gevraagd aan te geven of ze sneller (of langzamer) en efficienter (of niet efficienter) met twee beeldschermen dan met één beeldscherm konden werken. Op het vragenformulier was naast de vragen ruimte overgehouden voor opmerkingen.
Procedure
De proefpersonen werd voor het experiment verteld dat ze deel gingen nemen aan een onderzoek in het kader van het derdejaars vak 'Onderzoeksopdracht'. Zij werden erop gewezen de instructie goed te lezen, ook werd hen meegedeeld dat hun gegevens vertrouwelijk behandeld zouden worden.
De proefpersonen doorliepen individueel het programma, dat begon met de eerder genoemde instructie. Er werd hen gevraagd een taak uit te voeren, deze taak bestond uit het invoeren van één dosis van een bepaald medicijn, het starten van het model en het vervolgens invullen van de resulterende bloeddruk in een tabel op het scherm. Deze procedure moest nog vier keer met oplopende doses herhaald worden om de taak te vervullen. De juiste bloeddruk bij een bepaalde dosis moest ingevuld worden voordat met de volgende dosis verder gegaan kon worden. Om een volgorde-effect uit te sluiten zijn er twee condities gecreeerd: de ene helft van de proefpersonen maakte een taak eerst op één beeldscherm en maakte daarna eenzelfde soort taak op twee beeldschermen, de andere helft begon op twee beeldschermen en maakte daarna eenzelfde soort taak op één beeldscherm. Elke proefpersoon werkte dus zowel met één beeldscherm als met twee beeldschermen.
Nadat de proefpersonen de twee taken hadden voltooid werd hen gevraagd de vragenlijst in te vullen.
| Tabel 1. Gemiddelden en de standaarddeviaties van de werksnelheid in seconden voor één taak | ||||
|---|---|---|---|---|
| Tijd per taak in seconde | Tijd per taak in seconde | |||
| Volgorde: | n: | Eerste taak: | Tweede taak: | Mtotaal: |
| Van één beeldscherm naar twee beeldschermen | 18 | |||
| M | 549 | 438 | 494 | |
| SD | 123 | 26 | ||
| Van twee beeldscherm naar één beeldscherm | 18 | |||
| M | 506 | 431 | 469 | |
| SD | 94 | 101 | ||
| ------ | ------ | ----- | ||
| Mtotaal | 528 | 435 | 482 | |
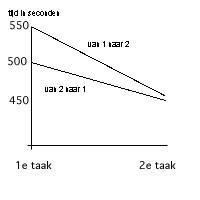
Ook Figuur 2 en Tabel 1 laten zien dat de tijd die de proefpersonen voor een taak nodig hadden afneemt.
Om deze eerste (voorzichtige) analyse te kunnen controleren is er een variantie-analyse voor herhaalde metingen uitgevoerd. De factoren bij de analyse waren Volgorde (deze bestond uit de twee condities: van één beeldscherm naar twee beeldschermen en van twee beeldschermen naar één beeldscherm) en Tijd (deze bestond uit de totale tijd nodig voor de eerste taak en de totale tijd nodig voor de tweede taak). Hierdoor kon er getoetst worden op: 1) volgorde-effect; 2) effect van leren op de werksnelheid en 3) interactie-effect. Het interactie-effect is het effect van het aantal beeldschermen omdat er bij het interactie-effect de resultaten van de proefpersonen in de volgorde-conditie 'van één naar twee beeldschermen' op hun eerste taak en de resultaten van de proefpersonen in de volgorde-conditie 'van twee beeldschermen naar één beeldscherm' op hun tweede taak (voor beide groepen zijn dat de resultaten op de taak met één beeldscherm) vergeleken wordt met de resultaten van de proefpersonen in de volgorde-conditie 'van één beeldscherm naar twee beeldschermen' op hun tweede taak en de resultaten van de proefpersonen in de volgorde-conditie 'van twee beeldschermen naar één beeldscherm' op hun eerste taak (voor beide groepen zijn dat de resultaten op de taak met twee beeldschermen). Bij deze vergelijking wordt rekening gehouden met de volgorde- en leereffecten. De resultaten van de analyse staan in Tabel 2.
| Tabel 2 Variantie-analyses |
|---|
| F ratio | p* | |
|---|---|---|
| Between-Subjects effect Volgorde | 1.32 | .26 |
| Within-Subject effect Tijd | 16.89 | .00 |
| Interactie Volgorde by Tijd | .61 | .44 |
Uit deze resultaten blijkt er geen significant effect is van de volgorde waarin de proefpersonen werkten. Het maakt dus niet of je de eerste keer of de tweede keer met één dan wel twee beeldschermen werkt. Verder is te zien dat er een significant verschil is tussen de eerste en de tweede taak als men kijkt naar de werksnelheid waarmee de taken zijn uitgevoerd. De tweede taak wordt aanzienlijk sneller uitgevoerd dan de eerste taak, er is dus sprake van een leereffect. Een interactie-effect tussen volgorde en werksnelheid kon niet worden vastgesteld, dit betekent dat er geen verschil is tussen de werksnelheid op één beeldscherm en de werksnelheid op twee beeldschermen.
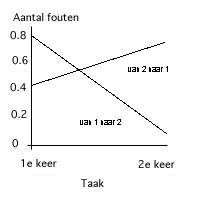
In Figuur 3 en Tabel 3 is het gemiddeld aantal fouten dat gemaakt werd, per conditie, te zien. Er is een interactie-effect tussen het aantal fouten en de volgorde-conditie. Zie vooral Tabel 3. Het wil zeggen dat het aantal beeldschermen waarmee de taak werd uitgevoerd, invloed heeft op het aantal fouten dat gemaakt werd.
| Tabel 3. Gemiddeld aantal fouten bij het uitvoeren van een taak |
|---|
| Taak | ||||
|---|---|---|---|---|
| Volgorde: | n: | Eerste taak: | Tweede taak: | Mtotaal: |
| Van één beeldscherm naar twee beeldschermen | 18 | |||
| M | 0.78 | 0.06 | 0.42 | |
| Van twee beeldscherm naar één beeldscherm | 18 | |||
| M | 0.44 | 0.66 | 0.55 | |
| ------ | ------ | ----- | ||
| Mtotaal | 0.61 | 0.36 | 0.49 | |
Er is een variantie-analyse voor herhaalde waarnemingen uitgevoerd om te bepalen of er significante effecten zijn. Ook bij deze analyse waren de factoren Volgorde (deze bestond uit de twee condities 'van één beeldscherm naar twee beeldschermen' en 'van twee beeldschermen naar één beeldscherm') en Tijd (deze bestond uit het aantal fouten op de eerste taak en het aantal fouten op de tweede taak). Hierdoor kon er weer getoetst worden op: 1) volgorde-effect; 2) effect van leren op het aantal fouten en 3) interactie-effect (d.i. het beeldschermeffect). De resultaten van de analyse staan in Tabel 4.
| Tabel 4. Variantie-analyses van het aantal fouten |
|---|
| F ratio | p* | |
|---|---|---|
| Between-Subjects effect Volgorde | 0.41 | 0.53 |
| Within-Subject effect Tijd | 1.22 | 0.28 |
| Interactie Volgorde by Fout | 4.35 | 0.045 |
Uit deze analyses blijkt dat er opnieuw geen effect is van volgorde, en dus dat er geen verschil is tussen personen die eerst met één beeldscherm werkten en daarna met twee en zij die eerst met twee beeldschermen werkten en daarna met één. Ook is er geen verschil tussen het aantal fouten dat er op de eerste en op de tweede taak gemaakt werd, er is dus geen effect van het leren op het aantal fouten dat gemaakt wordt. Er is wel sprake van interactie tussen het aantal fouten dat gemaakt is en de volgorde waarin gewerkt is, dit betekent dat het aantal beeldschermen waarmee een taak wordt uitgevoerd effect heeft op het aantal fouten dat gemaakt wordt. Deze gegevens gecombineerd met de gegevens uit Tabel 3 levert de conclusie dat de proefpersonen met één beeldscherm significant meer fouten maken dan met twee.
| Tabel 5. Resultaten van de vragenlijst |
|---|
| Vraag | n 1) | Gemiddelde | SD | 95% b.i | rit |
|---|---|---|---|---|---|
| 1. makkelijker | 35 | 2.03 | 0.95 | (1.72; 2.34) | 0.59 |
| 2. niet omslachtiger | 35 | 2.34 | 1.19 | (1.95; 2.73) | 0.43 |
| 3. prettiger | 35 | 1.63 | 0.97 | (1.31; 1.95) | 0.63 |
| 4. niet vermoeiender | 35 | 2.20 | 1.11 | (1.83; 2.57) | 0.59 |
| 5. overzichtelijker | 35 | 1.71 | 1.15 | (1.33; 2.09) | 0.28 |
| 6. sneller | 36 | 2.14 | 1.12 | (1.77; 2.08) | 0.57 |
| 7. efficienter | 36 | 1.97 | 0.86 | (1.69; 2.25) | 0.47 |
| ------ | ------ | ------ | ------------ | ------ | |
| Totaal | 36 | 2.00 | 0.69 |
Deze gegevens lijken aan te geven dat er bij de proefpersonen een lichte voorkeur is voor Twee beeldschermen, immers op de 5-puntsvragen duidt een gemiddelde score van 2 op een voorkeur voor twee beeldschermen.
Om het gebruiksgemak te kunnen vergelijken met de twee volgorde-condities zijn de verschillende antwoorden per bij elkaar genomen tot één individuele score op gebruiksgemak. Vervolgens is met behulp van een T-toets gekeken of de gemiddelden (zie Tabel 6) per volgorde-conditie verschillen.
| Tabel 6. Gemiddelden gebruiksgemak | |||
|---|---|---|---|
| Volgorde | n | p* | |
| Van één beeldscherm naar twee beeldschermen | 17 | ||
| M | 1.92 | ||
| SD | 0.50 | ||
| 0. 509 | |||
| Van twee beeldschermen naar één beeldscherm | 18 | ||
| M | 2.08 | ||
| SD | 0.84 |
Uit Tabel 6 blijkt dat er geen verschil is in het gepercipieerd gebruiksgemak tussen de twee volgorde-condities. Dus proefpersonen die van één beeldscherm naar twee beeldschermen gingen hebben niet een ander beeld van het gebruiksgemak van twee beeldschermen ten opzichte van één beeldscherm dan de proefpersonen die van twee beeldschermen naar één beeldscherm gingen.
Er is een verschil tussen de werksnelheid bij de eerste taak vergeleken met de werksnelheid bij de tweede taak, er is dus sprake van een leereffect. Bij dit onderzoek is getracht dit leereffect te voorkomen door de proefpersonen te laten oefenen met de taak. Uit het feit dat de tweede taak significant sneller is uitgevoerd dan de eerste taak blijkt echter dat deze oefening niet voldoende is geweest. Dit gegeven zou er voor kunnen pleiten om bij vervolgonderzoek te werken met geoefende proefpersonen die de taak volledig beheersen. Op deze manier is het mogelijk de leereffecten te elimineren en zo alleen naar de effecten van parallellisme te kijken.
Uit de analyse van het aantal fouten dat per conditie gemaakt werd blijkt dat er geen effect is van volgorde, dit wil zeggen dat in beide volgorde-condities er geen significant verschil is in het aantal fouten dat gemaakt werd. Er is echter wel sprake van een interactie effect, de taken uitgevoerd op één beeldscherm bevatten significant meer fouten dan de taken uitgevoerd op twee beeldschermen. Wanneer een taak wordt aangeleerd op twee beeldschermen is het onverstandig om eenzelfde soort taak uit te voeren op één beeldscherm. Omgekeerd geldt dat wanneer een taak op één beeldscherm wordt aangeleerd, er minder fouten gemaakt worden als deze taak later op twee beeldschermen wordt uitgevoerd.
Wanneer we het voorgaande samenvatten dan kan gesteld worden dat de proefpersonen niet significant sneller of langzamer gewerkt hebben met twee beeldschermen dan met één beeldscherm. Wel worden er meer fouten gemaakt wanneer er met één beeldscherm gewerkt wordt. Een vreemd verschijnsel is nu dat dit meer maken van fouten niet leidt tot een lagere werksnelheid. Een mogelijke verklaring hiervoor is dat er door een klein aantal proefpersonen een groot aantal fouten is gemaakt. Hierdoor wordt het gemiddeld aantal fouten, wat erg klein is, flink omhoog gehaald. De werksnelheid van deze proefpersonen is ook lager, echter het effect van deze lagere snelheid op de gemiddelde snelheid is kleiner dan het effect van de grote hoeveelheid fouten op het gemiddelde aantal fouten.
De vragenlijst, die naar de mening van de proefpersonen over het gebruiksgemak van twee beeldschermen ten opzichte van één beeldscherm vroeg, geeft aan dat de proefpersonen het gebruiksgemak van twee beeldschermen hoger inschatten. Hierbij moet worden opgemerkt dat het voor de meeste proefpersonen de eerste keer was dat ze met een computer met twee beeldschermen werden geconfronteerd. Het werken met twee beeldschermen zou daardoor in het voordeel kunnen zijn ten opzichte van het werken met één beeldscherm omdat het 'nieuw' is.
Een opvallend detail is dat proefpersonen op de vragenlijst aangeven dat ze denken met twee beeldschermen sneller te kunnen werken dan met één beeldscherm. Uit de gegevens van het experiment blijkt dat dit niet het geval is.
Enschede, 1996; updated aug. 2002; updated 2005.
Dirkzwager, A., & Mol, M. (1987). Onderwijskundig computergebruik. Amsterdam: Addison-Wesley.
Egan, D. E. (1988). Individual differences in human-computer interaction. In M. Helander (Ed.), Handbook of human-computer interaction (pp. 543-565). North-Holland: Elsevier Science Publishers.
Min, R., Kan, H., van & Struyker Boudier, H. (1982). Computer simulation programs in problem-oriented medical learning at the university of Limburg. Computer & Education, 6, 153-158.
Min, F.B.M. (1994). Parallel Instruction, a Theory for Educational Computer Simulation. Unpublished manuscript, Universiteit Twente, Faculteit Toegepaste Onderwijskunde, Enschede.
Min, F.B.M. (1996). Parallellisme bij werk-, leer- en doe-omgevingen: De parallelle Instructie Theorie voor coaching en Open leeromgevingen voor simulatie. Unpublished manuscript, Universiteit Twente, Faculteit Toegepaste Onderwijskunde, Enschede.
Moore, J.L. & Thomas, F.H. (1983). Computersimulation of experiments: a valuable alternative to traditional lab work for secundary school teaching. School Science Review, 64(229), 641 - 655
Rivlin, C., Lewis, R., Davies-Cooper, R. (1990). Guidelines for screen design. Oxford: Blackwell Scientific Publications.
