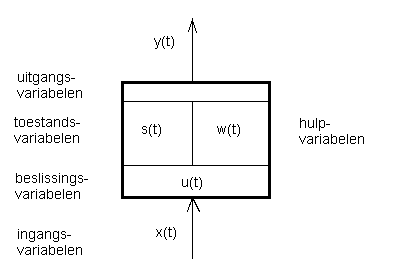
Figuur 1. De systeemcel (Hanken & Reuver, 1977; Vos & Min, 1998). Een systeem of een model van een systeem kent de volgende soorten variabelen: ingangs-, beslissings-, toestands-, hulp- en uitgangsvariabelen.

Door Rik Min.
Key-words: systemen, modellen, variabelen, hulpvariabelen, toestandsvariabelen, geheugenelementen en startwaarden.
Samenvatting
Dit artikel gaat over modellen en wat daarbij komt kijken. Veelal worden modellen als black-box gerepresenteerd waarbij allerlei soorten variabelen op een bepaalde plaats worden gesitueerd. Met deze theoretisch correcte voorstelling van zaken starten we hier dan ook. Maar gaande dit artikel worden met name de beslissingsvariabelen uit de black-box gehaald en op een andere manier gesitueerd. Er ontstaat dan een iets andere black-box, een met een exclusieve feedback-loop en een duidelijke benoembare, exclusieve besturing-module (de besturing). We noemen beide benaderinswijze meta-systemem (Vos, 1994). Dat heeft voordelen, want van feedback-systemen is theoretisch aangaande gedrag, stabiliteit en daarmee verbandhoudende eigenschappen zeer veel bekend. Uit de regeltechniek is bekend dat elk feedback-systeem feitelijk hetzelfde karakteristieke regel-gedrag heeft. Dit soort voordelen passeren hier dan ook de revu.


Deze voorstelling van zaken is te herleiden tot een meer gebruikelijke manier van voorstellen, namelijk met een feedbackloop en een beslissingsmoment.
Daarom zijn hier figuur 3 en 4 toegevoegd. In figuur 3 is te zien dat (een) beslissingsvariabele aan de ingang is gesitueerd. Dat is in de regeltechniek gebruikelijker. De (een) toestandsvariabelen wordt rechtstreeks uitgevoerd zodat de (een) uitgangsvariabele y(t) feitelijk de toestandsvariabele is geworden.
Als we ervan uitgaan dat elke y(t) als volgt beschreven kan worden:
a(t) zijn parameters, die eventueel veranderen kunnen in de tijd. In de hier volgende figuren is te zien dat het bestuurd systeem nu de black-box is. Deze black-box heeft als uitgangsvariabelen y1(t), y2(t), enz. Hij bevat verder (gewoon) alle hulpvariabelen w1(t), w2(t), enz, de toestandsvariabelen s1(t), s2(t), enz, maar niet meer (een van) de beslissingsvariabelen u1(t), u2(t), enz. Voor elke beslissingsvariabele is er in dit nieuwe meta-model een feedback-loop en een comparator bijgekomen; een vergelijkingselement die de gewenste waarde kan vergelijken met de gemeten waarde.
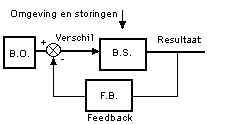
In figuur 3 ziet u het nieuwe algemene meta-model met het besturend orgaan en met de feedback-lus. Als het besturend orgaan zijn set point instelt op een ander (beter?) reultaat dan zorgt de comparator - die het verschil e(t) berekent tussen het resultaat y(t=n) en het set point u(t=n) - dat e(t) gelijk aan nul wordt. In figuur 4 is dit in de tijd te zien en grafisch in de tijd uitgezet.
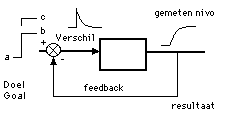
Figuur 4. We kunnen in deze figuur zeggen hoeveel het verschil is tussen de gewenste en de gemeten waarde.
Figuur 4 laat ook zien dat als het set point door de beslissers van a op b wordt gezet (of c) dat dan het resultaat deze gewenste waarde langzaam of snel in de tijd weet te bereiken. De snelheid waarmee dat bereikt wordt, hangt van de interne tijdconstantes af. Als het verschil nul wordt stopt de drijvende kracht die het bestuurd systeem 'drijft'; en is het model in rust ('steady state'). Dit meta-model is door Min op de computer gesimuleerd. (Zie elders.) De tijdconstantes zijn hierbij belangrijk en derhalve instelbaar. Ze hangen af van andere modelgrootheden, met name van de parameters a1(t), a2(t), enz. Ook de startwaardes van de toestandsvariabelen zijn bij deze simulaties (natuurlijk) allemaal instelbaar.
Min, R. (1998)
Verhandeling over leren. Op internet:
http://home.tiscali.nl/schopmanlanden.nl/Papers/LerenModel.html
Min, R. (1999)
Verhandeling over besturen & ontwerpen. Op internet:
http://home.tiscali.nl/schopmanlanden.nl/Papers/ontwerpen.html
