A CONCEPT MODEL FOR LEARNING
An attempt to define a proper relations scheme between instruction and learning and to establish the dynamics of learning in relation to motivation, intelligence and study-ability ('studeerbaarheid')
By R. Min, H. Vos, P. Kommers and C. van Dijkum.
- Rik Min, researcher, designer, multimedia & simulation - in education - specialist (*),
- Hans Vos, educational researcher and engineer (*),
- Piet Kommers, educational researcher (*) and
- Cor van Dijkum, modelling specialist (**).
(*) University of Twente: Faculty Educ. Science and Technology, PO Box 217, 7500 AE Enschede. The Netherlands
(**) University of Utrecht: Faculty Soc. Sciences, Heidelberglaan 1, 3584 CS Utrecht. The Netherlands
This article is published on paper in the Journal of Interactive Learning Research (the formal Journal of Artificial Intelligence in Education) Vol.11, no. 3/4, 2000, p.485-506.
Keywords: learning, models, modelling, model for learning, learning model, instruction, study-ability, motivation, incentives, instruction sources, means of instruction, learning tools, half-life-time, feedback systems and quality control.
This is the first what I call interactive scientific paper ('ISP') (perhaps in the world), because you can test - online - our hypothesis about some of our parameters on learning (knowledge accumulation and reaching a target) and getting answers on questions as "What is the influence of increasing motivation on the learning-time" or "What is the influence of decreasing study-ability on the learning-time?" (Answer: the half-life-time decreases.)
Summary
For years it has been attempted within educational science to establish the process of learning. A lot is known about instruction but as to learning and acquiring knowledge and insight we still relatively knows very little. A lot of research is carried out into methods of instruction but very little into learning with learning tools. In this paper an attempt will be made to do so. Discussions about: how can a learning process be turned into a model: how can learning be modelled? First there should be a concept model with the basic quantities and the relations between them so that scientists have something to go by in their discussions. Recently, a committee of the Minister of Education and Science with chairman Wijnen, introduced the political concept 'study-ability'. All the more reason to lay down the points of application of these concepts in a larger entity and conceptually in an understandable model.
Then we know what we are talking about; where every concept can be applied in the overall learning process. In this paper we want to construct a clear and irrefutable model, an analogon, to describe the phenomenon of learning. This might in the long run help us to get to the bottom of learning (with learning and instruction tools) with the attending circumstances. We consider learning as a relatively active activity of a pupil, instruction on the other hand as a relatively passive activity of someone or something in the role of teacher.
Introduction
In this paper we will try to investigate whether we can find and establish any relations between a number of modern concepts which present day policy makers apply in educational science and learning tools technology. Concepts such as study-ability and motivation should be made into a coherent frame so that an unambiguous and consistent model is created that can be reproduced. Designers of learning tools wants to have a qualitative and quantitative insight into learning or at the least into learning behaviour. In this paper we want to find reproducible insights and answers to questions such as: How is it that some learning tools have a motivating effect on a certain type of pupil? What is learning exactly? How does study-ability of the - curriculum and the learning tools available - influence independent learning? Where do these matters apply in the learning process? Learning can be summed up in four words: assessing, executing, becoming interested and starts always by doing something.
Traditionally little research is done within educational; science into drawing up deterministic models that can establish and copy phenomena which occur during learning or instruction. Conceptual models in the form of mathematical equations or analogons are rarely seen in particular. A lot of research is done into relations between design variables and learning effects in for instance teacher-pupil instruction situations or computer-based learning. But it can not always be traced with which and how much success. Let alone that researchers would publish their findings in respect of learning effects in mathematical models.
We would like to find answers on research questions like: 'how can motivation reduce the aversion against learning?' It appeared that motivation to attend 'boring' classes increases if good learning tools have been included in the curriculum. If the class offers 'differentiated learning tools' it will help motivate the pupil to study that subject well. Then there are questions such as: which forms of instruction and forms of feedback in simulation are best suited to promote the motivation to learn? Or a more topical question: how can good learning tools increase the study-ability of lessons. How can you increase study-ability and thus help decrease aversion in learning processes?
Definition: Model-driven (computer) simulation (MDS) is an open interactive learning environment (here) - based on a reality model - whereby the underlying mathematical model will ultimately determine how it will react on an action of a user (here: a learner).
Definition: An Intelligence Computer Simulation (ICS) is model-driven simulation with a rule base to monitor the dynamic behaviour of the model at every simulation step (dt) and which gives a special kind of (extra) feedback to the user, besides the usual feedback . (See fig. 5).
Definition: A learning model (LM) is an unambiguous established model (or analogon) (as yet qualitative) of phenomena (usually knowledge increase) as they occur when using learning or instruction tools.
Atkinson advanced a thesis in 1977 in the form of a differential equation. It was called a 'learning equation'. People spoke of the knowledge increase in Atkinson's learning equation. The theoretical basis for it lay in the 'broadcast process'. It was studied how information through the media is transferred and how information is diffused in a population of N persons. Parameters can be taken here as the percentage of the total population that is converted every time the (same) piece of news is broadcast.
If we consider how acquisition of knowledge or learning takes place, then a curve can be supposed - under influence of instruction or reading of a text - as indicated in figure 1. Atkinson's learning model has been known for years, as described by Anderson (1983). This learning model gives a model-like deterministic description of 'learning or knowledge increase' as it were. A closer analysis of this model reveals a differential equation of the type dq/dt=a(I-q), in which I is the input (stimulus) for instance an instruction and output q the actual knowledge and in particular its level, dq/dt is the increase of q in time. The 'increase' in this equation equals a constant percentage of what remains, i.e. what a person still has to learn. (I-q). The analogue solution for such equations is not considered here. We want to do a simulation study (on a PC) and therefore the differential equation on its own is already sufficient.
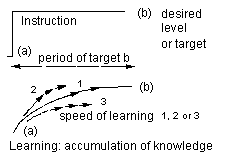
Figure 1. How does the learning process work? How fast do people absorb? Is absorbing the same as learning? Which parameters are responsible for this? Intelligence? The qualitative level of instruction? The goals one sets? How does the process of forgetting work? This figure shows that learning is accumulation of knowledge en forgetting is the reverse. We assume that there is an incentive somewhere or that someone has set himself to target (top figure) (input). This figure is qualitative if we consider these curves quantitatively, we see time constants that are different for each person and in each learning situation as indicated in the bottom figure.
This model also occurs in the 'diffusion comparison' of the 'broadcast process' (Vos & Min, 1997). Also in the increase of the load and voltage in a capacitor: du/dt=(1/RC)*(E-u). (See also the figure at the end of the paper.) The feedback model about diffusion of Lava and March (1975) and Spada and Kempf (1977) have that same structure. Kommers (1990) describes something similar in his thesis: the model of Anderson 'the architecture of cognition'. That model contains the equation da/dt=n-p*a. That is a differential equation. All these models are characterised by a first order differential equation in which the increase of the modelled variable (d.../dt) is determined by a stimulus (an input variable, for instance: I, E or n), by a person's characteristics (a parameter) and the actual value of that variable. In Atkinson's model this parameter is called 'intelligence' (a or in our case: 1/RC). If we consider all these models they are in fact analogous to each other. This article wants to keep that analogy and propose a new model. That new model will also contain the parameters: motivation, study-ability, forgetting, and being able to choose yourself from a differentiated offer of learning and instruction tools (the incentives). See also the (stochastic) models of Bush and Mosteller (1995).
Within educational science increasing use is made of electronic learning tools. First there were only the linear learning tools such as instruction films through tv stations or later video recorders. Now there are interactive dynamic multimedia learning tools on cd rom, cd-i or the World Wide Web.

Figure 2. A wants to tell B something; or B wants to know something from A, the question is, however: does it work and does B remember everything?
The first work from an idea of 'supply' of instruction tools. The second from a sort of 'demand' idea for instruction. It is striking how little we know of the learning effects that these media have on the student. Within (traditional) educational science we know a lot about instruction but little about absorbtion, processing knowledge and acquiring insight. That is we know little about active learning and the accompanying learning processes, resistances and how motivational design variables can anticipate.
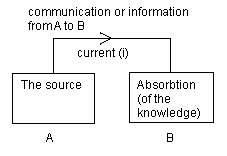
Figure 3. Knowledge is absorbed by a pupil; but when does it go easily and when more difficult; and how do you get the best results?
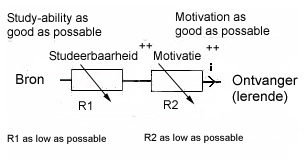
Figuur 3b. The important political and educational concepts as 'motivation' and 'study-ability' are resistances 'against an optimal knowledge flow'; and can be situated 'in serie'. If the motivation is low; then you can say: "the resistance against teaching source is high". Omgekeerd als de studeerbaarheid goed is, is de weerstand tegen het aangebodenen dus laag. Deze weerstanden staan dus in serie tussen de bron (A) en de lerende (B).
Instruction tools are usually well thought-out but open learning environments. Little is known about the actual way learning and brain function. One of the things that are lacking in contacts among researchers, is a proper valid model of learning and the accompanying learning process. We know that good learning tools reduce the' resistance against learning'. We want to take that literally here and discuss old ideas about 'forgetting' and 'remembering' of Meerling (1981). We want to discuss new ideas about how to remove resistance against boring lessons by using learning tools - for instance multimedia computer simulations or games - to create something that other tools can't. Such an approach might bear fruit in the scope of discussions about a 'supply of learning tools that is as varied as possible'. Only recently, B. Richmond published a paper on internet on 'content assimilation' (1998). The combination of this type of learning tools together with more traditional boring instruction tools might yield a successful cooperation. We want to enter this discussion based on a conceptual model; an analogon. For then everyone knows what we are talking about - in a qualitative sense - and where exactly in the whole, process our learning and instruction tools become effective in the whole process. Then we can map research variables and conditions (qualitative). Perhaps we shall be able to collect qualitative data some time in the future.
At present it is considered not done to do research into models about learning. Many educationalists consider it as a waste of time. H. Schmidt conducted a study into models quite recently (1998). He came across the 'modal model'. A model that recognizes two components: one for the short term memory and one for the long-term memory. This model is based on ideas (according to Schmidt incomplete) on forgetting by Ebbinghaus (Schmidt, ORD '98 conference 1998, Enschede). Yet the need to make a new start in this field is making itself felt, the need for new conceptual model about learning.
This article describes a basic model of learning or an analogon. This model was drawn up by the University of Twente in cooperation with others. This model distinguishes the separate parts and a few assumed basic principles as can be distinguished in learning and the learning process. This rough first draft can possibly provide an incentive for the discussion about learning and learning tools. Research into effects of learning and a useful scientific discussion about it are only feasible if the actors and dynamics are clearly set out. With such a model one can indicate where the learning tools are effective and where they result in.
Instruction versus learning
For years we have tried in educational science to understand the process of learning with learning tools such as simulation. We know a lot about instruction; but little about learning and acquiring knowledge and insight. The right balance between open learning environments and instruction is essential in simulation. To start with, there should be a model with the basic issues. This is what this article is trying to achieve. The research have to be about: how can a model be made of the process of learning: how can learning be modelled? We want to construct a clear irrefutable model, an analogon so as to learn how this phenomena can be described and hopefully to be able to understand it better.
The model should also establish a background about how learning takes place with learning tools. In the course of the years - while we were working on learning tools for simulation - we have begun to understand what is actually achieved in pupils with simulation: not knowledge transfer but motivation and the drive to further study.
Theory in respect of instruction is different from theory in respect of learning. Experts in this field, the 'learning technologists' have developed good ideas that are often at right angles with ideas from the traditional world of instruction 'the instruction technologists'. This has of course to do with the fact that instruction is the supply side because it has something to offer and learning is acquiring knowledge by the user, the demand side in education. The 'demanding information' and 'supplying information' are traditional. Ideologically, however, they are two entirely different fields of science. This becomes obvious when one compares the ideas of Gagné and Romiszowski with those of Van Parreren and Papert. The latter have thought with student-controlled learning as their starting point. Starting points approach and the goals in their solutions for educational problems are rather different as compared with those of the classical instruction technology.
In the world of educational technology there are two different fields: that of 'learning technology' and that of 'instruction technology'. Properly speaking, there are designers of learning tools and designers of instruction. It is essential for the understanding of the analyses below that a clear distinction is made between 'learning tools' and 'instruction tools'. In principle, learning tools do not contain any knowledge or very little whereas instruction tools do. If learning tools do contain knowledge, then we have a combination of a learning tool with an instruction tool. Or else the underlying systems or models should be called knowledge. But that is not the point here even though it occurs frequently in practice. In this article however, those two functions should be clearly separated and analysed.
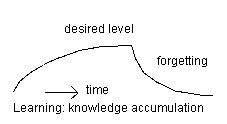
Figure 4. Learning and forgetting; knowledge accumulation and residual knowledge. A pupil sets himself a goal; when it has been achieved he/she stops with learning; the level of knowledge, skills or insight which he/she had set him/herself has been reached.
Our idea begins with a proper division of types of educational software. To start with a clear distinction should be made between learning and instruction tools. Learning environments are not instruction environments. Learning tools such as simulation have the effect that given a proper case the user will acquire a good attitude in respect of the subject and he will want to continue: attending a class or reading a book.
Thesis: There is a big difference between learning tools and instruction tools
Thesis: Instruction tools are one-way environments; learning tools are two-way environments.
An example that illustrates this principal difference between instruction-rich and instruction-poor is the bare classroom for chemistry practicals in a chemistry lab where there is no knowledge transfer other than that manuals are studied. Opposed to that is a course on television where knowledge is transferred when taught in a specific way, although there is little or no interaction. These are the two extremes: learning tool versus instruction tool.
If a simulation functions properly, the user will become motivated to do a further study in a (boring) book or in a (boring) continuation course. Learning tools should be seen as work environments - just like practicals - where you learn how to handle already acquired knowledge. Pieces of the jigsaw will automatically fall in the right place if all goes well and a proper casuistry is used. In our model, instruction is seen as a source from which someone can 'drink'.
Thesis: Learning tools should motivate to real learning and further study
The primary goal of a learning tool like a computer simulation program should be motivation for possible further study in boring books or dull lessons. In our type of learning tools and simulation programs learning comes only second. A computer simulation program should increase the insight into a matter. Students should be taught to think in a wider perspective; he should see the cohesion between things. Present knowledge and insights should be strengthened; the learner should learn to think in concepts. There is one part in our model that stimulates this motivating process. If motivation is zero nothing is learned, if motivation is tops people learn fast.
Computer simulation programs 'teach one by doing'. Because one is working on a task or case one learns. A simulation environment is a 'do' and 'work' 'environment' at the same time. Computer simulation programs and other learning tools are important to organise a curriculum in such a way that students are offered differentiated learning tools. This guarantees the individual student that he can follow the right learning course. It helps break the curriculum's or learning program's monotony. It is purely for personal change (optional) and because some students can be better motivated this way (possibly because of the different approach; perhaps because of their visual or auditive preference for the one or the other learning tool).
The continuation of the learning process
It has been suggested earlier by Min (1992 and 1994) that proper instruction is absolutely essential for a bare learning tool such as 'common' simulation programs. There should at least be some good assignments or cases provided with a bare model-driven computer simulation.
He poses in one of his articles (a testable hypothesis) that learning with a learning tool should be set in motion by proper 'instruction' (texts, pictures, instruction or video instruction). A well proportioned learning tool with proper feedback (textual. graphic and/ or dynamic) should keep that learning process going.
The figure below actually represents a simplified version of the above complex situation. It shows how a learning process is 'set going' by incentives (all kinds of instruction) and 'is kept going' by all kinds of feedback, like 'messages', 'intelligent video fragments', 'growing graphs' etc.. Learning is obviously a feedback system in which 'one learns until the desired level is achieved' (Min, 1992, 1994, 1996)
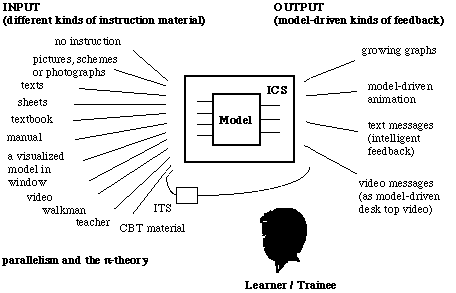
Figure 5a. Input and output process for a learning process that should be kept going. On the input side the different kinds of instruction (manuals, pictures, teachers, etc.) and on the output side of a 'learning process' the different kinds of feedback (graphical, texts, etc.).
(An example: video and other kinds of instructons as 'input' and video feedback as 'output' at a 'learning session'.)
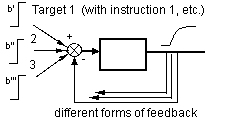
Figure 5b. Figure 5a can be interpret by scheme 5b. Schematic idea about 'parallelism' and the 'parallel instruction theory' of Min: on the input side of a learning environment a lot of instruction types and/or formats are possible and on the output site did a lot of model-driven feedback forms are possible. And every thing in common and/or parallel (Min, 1994)
The following rule applies to all designers: the a-synchronic simulation processes on the 'input side' and on the 'output side' of this learning environment, they all need to be in the user's view and must be presented parallel (Min, 1994)
Thesis: Setting a learning process in motion (with a 'bare' learning tool content wise) takes place (or should take place) by proper instruction (in the form of assignments, booklets, cases, self-instruction etc.)
Thesis: Keeping a learning process going (with a content wise 'bare' learning tool) should be achieved by proper textual and graphic feedback.
A poor and non-intelligent learning tool can never keep a learning process going. If one has scored sufficiently, a new challenge should be presented in the form of an assignment or a case. Then we come full circle. An instruction will then be 'input' for the learning process and the output on an intervention into a learning tool is feedback on the action of the learner.
Definition: Parallelism is a concept which is applied by designers of work- and learning environments. As much information as possible (and desirable) is presented at as; large a scale as possible. Everything can be compared to everything else and the (brief) memory of the user does not need to be consulted. (The automatically large screen of SUN computers and control rooms of operators illustrate this).
Definition: The Pi theory is a design theory which - from cognitive psychology - offers an explanation why the concept of parallelism is essential in combined learning and instruction tools. (Looking back, this theory can explain why ms-dos computers failed as learning tools for the greater part.)
Learning models
In 1992, Min carried out a pilot research project into 'learning models' (LM) in computer simulation. See for an example figure 6.
Figure 6. One of the five 'learning models' for a qualitative idea how pupils learn in simulation learning enviroments.
Such 'learning model' (LM) is not identical to a 'model for learning'. He has set the concept aside for something quite different. That is why in this article we have systematically used the description: 'a model for learning" or rather "a model in respect of learning'. Min presents five learning methods that can be applied in learning with computer simulations. These methods are 'discovery learning', 'learning by doing exercises', 'guided discovery learning' (with intelligent computer simulation; ICS), 'problem oriented discovery learning' (similar to 'problem solving') and 'learning by doing - scientific - experiments' (Min, 1992).
At the time he distinguished five 'educational types of usage' of (model-driven) simulation programs (also acquired by research) and thus there were five 'types of learning' too. Those models were called learning models (LM). Those five models had been drawn up based on observations of learning behaviour. The experiments were carried out in observation rooms at Educational Science. They were filmed by three video cameras, twenty testees participated. Analyses of the tapes took one year. Through those the qualitative learning models could then be converted into quantitative learning models. Later (in 1996) students also carried out a pattern recognition study on the data. It yielded some useful results, but the material has not yet been exhausted. This was reported in 1992 (Min, 1992) (Groenewoud & Ter Burg, 1996) at the 'Healthy Education Conference' organised annually by the Dutch Society for medical education. However, it seems that there are similarities between the conclusion then and those of the present in this project of how to draw up an analogon of learning. In the future we hope to be able to illustrate the similarities between those two different approaches. For the present there seem to be two different opinions. If we match it with ideas the current diagrams are in fact feedback systems - which can be proven - then it should be quite possible to find those similarities. See in this respect the pictures and text in the educational material of the course 'Systems approach in educational science' by Vos and Min (Vos & Min, 1997).
Definition: A learning model (not to be confused with 'a model for learning') is a currency diagram in which the behaviour of a learner who uses simulation programs can be recorded (but not explained) (in Min, Gezond onderwijs congres, 1992).
A resistance-network as a model
Our thesis (hypothesis) is that instruction or an instruction tool can be compared to a voltage supply (or possibly a currency supply). The student can be compared to a control system (based on an integrating network) that is active until one knows something or can do it. The pupil can also be compared to the accumulation of a load in a 'condensator'. The integrating network or 'capacity' of a condensator is an 'analogon' for 'acquiring knowledge' (including concepts such as intelligence or memory. Acquiring knowledge -or in this case learning - can be compared with the charging of a condensator or the final process in a feedback system on the basis of an integrating network (with a specific time constant).
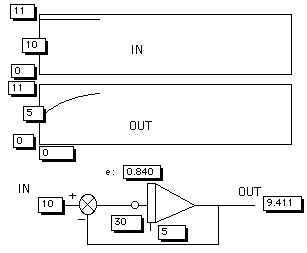
Figure 7. The heart of the analogon - the transfer function from input to output - simulated on a PC. The transfer function of this model is of the du/dt=1/RC (E-u) type. You should realise that e=E-u. Here e=IN-OUT. The integrator will go on integrating until e=0. At that moment u=E or OUT=IN. So this model could be a model for knowledge acquisition.
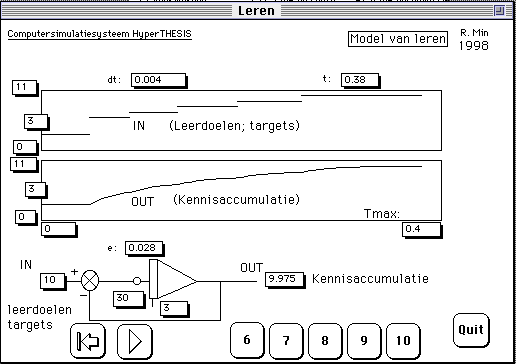
Figure 8. A slightly expanded model for acquisition of knowledge. Program 'LEARNING', version 2.0x. You see in this simulation program in which the model for learning has been included that there are a number of targets which the student can set himself. Then on will achieve a certain level of knowledge. You start at level 5 and chooses level (or target) 6,7,8,9, or 10. In this example one chose level 5 at the moment in time t=0 and on t=0.1 the target level was 9. (The begin level of the student was 3.) You can see that the student reaches the levels after acertain time.
Charging a condensator is actually similar. (See the mathematical equation of both systems; they are similar: that is 'they are analogous. There is isomorphy (term found by Ashby, 1956) between the simulation model of a feedback system (that goes on doing something until e=0), the (classical) model for charging a condensator and a (conceptual) model of knowledge accumulation, i.e. learning. We are aware of the specific limitations of these assumptions but if you are not prepared to assume something, a model case becomes impossible to draw up. Such models and concepts are dealt with in the course 'Methoden leer' with stochastic models in the curriculum of TO. Adaption says that a student learns something every time (on top of what he already knows; i.e. all through life one learns and there is a continuous accumulation. (Vos, 1997)
Figure 9a. The interactive simulation model. Left for experimental work; right for references.
Here you can start - by clicking - the interactive model of learning of Min (febr. 2000) as described in the text.
Case 1: If you change the 'target' ('IN') from '3' to '6' you see the outcome depends on 'studeerbaarheid' ('study-ablity') (R1) and 'motivation' (R2). Stop if the target is reached. Than you have to decrease R1 and/or R2 and than put the target to 9 the 50%-time cost twice as much than before (case 2). You see that 'duration of learning' (the 'leaning traject') is just the time until the difference between target and output (difference) is about zero. We call it the 100%-time. (The 50%-time - or half-life-time - is the time - in weeks - the target is reach at 50 procent.) Alpha says to what extent the slope is. In black you see a reference: the output with the normal parameter values.
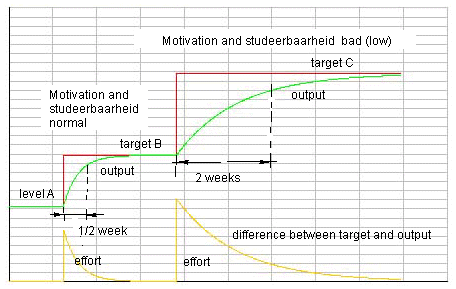
Figure 9b. A screendump (1) of the interactive simulation model above. You see two experiments: setting target B after 1 week and setting target C about 4 weeks. In the first experiment you see the target is reached quicker - at 80% of the target - than in the second experiment (later) at 80% of the target (1/2 week versus 2 weeks). In the second experiment the 'study-ability' (R1) and the 'motivation' (R2) are more worse so it takes more time to learn everything. When the study-ability increases (and here the resistance against, R1, decreases) learning will become potentially easier.
Do this - in your own way - by clicking on the button above.
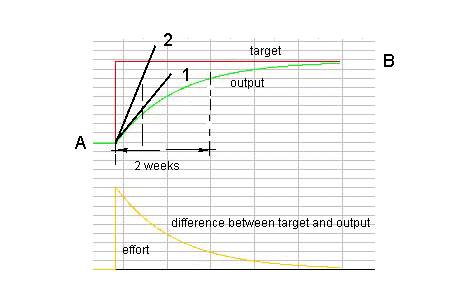
Figure 9c. A screendump (2) with the output of our analogon: our model of learning. This screen dump shows that - with a poor motivation to learn something and poor study ability - the learning time, the time to get from A to B, and to reach target B - is for instance two weeks - (see green curve with tangent 1). With our model of learning it can be simulated that with a better or good motivation and a better or good study ability, the learning time will be much shorter (tangent 2). The yellow curve shows that the difference between the measured value (green) and the desired value (red) is high at the beginning but it becomes smaller in the course of the process. Then, when the student fully understands the assignment, he stops learning and the teacher should give him a different assignment or challenge.
We first (in 1994) saw our 'learning model' as a link between a condensator with a resistance. We think that a RC network is a good analogon for the basic principles in the voltage field between learning with a learning tool and the use of an instructor during that process. In this model the condensator 'is' a 'model' of the student.
The 'capacity' of a condensator can be compared to brains, memory or intelligence. Thus learning can be compared with charging a condensator. If the capacity is large then the capacity for learning is large. If the capacity C is small, the capacity to learn is also small.
It is natural that a student feels a certain resistance towards learning. That is the resistance R2. Both 'wanting to learn while discovering' and 'wanting instruction' are hard work. A learning tool can contain oral instruction, but a manual or an assignment may not always be clear. The resistance against that can be removed by means of a well designed instruction tool. The resistance which a teacher or an instructor notices in a student is represented by the resistance R2.
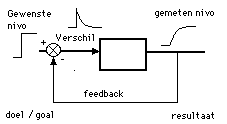
Figure 10. Second type of analogon a feedback regulation system. This is in principle the underlying system in learning as described by Scheiblechner and in 1997 by Vos and Min in their lectures for the course 'System approach in Educational Science' (1997) at the University of Twente. The pupil is offered an incentive and will continue until the difference between the 'knowledge in the incentive' and the 'knowledge in his head' is zero. The difference in a feedback system always goes to zero. The appropriate curve occurs in many places in social sciences, psychology and physics. In reality there is a multitude of stimuli. (See further down in the text and with the figures). But there is also a multitude of 'targets' and 'feedback systems'. The sum and substance of all this activity and knowledge accumulation is therefore 'learning' . If a person sets himself various goals (learning goals' etc.) you can use the term dynamic targets or standards. With single targets (or standards) one can continue to say a static target or norm.
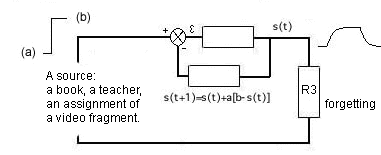
Figure 11. Ditto, as above. This representation is similar to the representation Atkinson (1977) gives in his learning equation. His model present how the learning or knowledge increase could progress in a pupil in the time given an incentive b: the total material to be learned. For comparison also see the model of 'diffusing equations' in the broadcast model of Lave and March (1975).
The second resistance - (R3) parallel to the condensator - is the leakage 'resistance' over the condensator and it symbolises 'forgetting'. The proper use of a learning tool will reduce the resistance against learning and will take effect on resistance R2. A proper instruction in a learning tool is important to get the learning process going. This is symbolised by a (voltage) source (source 1, source 2 of source 3). The model of how learning progresses under influence of the learning tool and instruction can be seen in figures 12 or 13. Thus this analogon has become a proper quantitative model for learning.
Summarising we can put a number of things that are essential in a learning process, knowledge transfer or knowledge acquisition opposite their analogous components:
- instruction as a source or voltage supply (source);
- knowledge accumulation - the learning process - as a feedback system or a condensator (C);
- communication as a stream (i);
- 'resistance against learning' (i.e. 'motivation') as a resistance (R2);
- study-ability as a resistance (in series) (R1).
It follows that Ohm's Law applies here as well. So U=i.R. As a resistance decreases or 'motivation increases' then learning will be easier. The resistance against learning (i.e. 'motivation to learn') (as a function of R2 or better 1/R2) can partly be removed by proper learning tools. The study-ability (as a function of R1 or rather 1/R1) can increase by a proper streamlined management in the curriculum and an adequate and specific supply of instruction and learning tools. When the study-ability increases (and (here) the resistance against, R2, decreases) learning will become potentially easier. Ohm's law says that with a certain voltage (U) the currency increases (I) when the resistance (or one of the resistances in series) decreases.
Thesis: Study-ability is (according to the Wijnen committee of the Dutch governement) the task of the universities to enable the student deal properly and swiftly (with his limited time, incomprehensible timetables, incomprehensible learning texts and learning tools) and they should not make a learning process more difficult than necessary.
Thesis: A resistance against learning occurs when unnecessary barriers occur in the course of a study. Suppliers of education and designers of learning tools should try to keep the resistance against (their) education and (their) learning tools as low as possible from the very start.
Anderson (1983) indicates in his ACT model ("adaptive control of thought') how knowledge (both declarative and procedural) is activated in semantic networks consisting of knots and sources; in other words how knowledge diffuses. The difference with our model is that there is no (charge-)source but there are various sources and influences (e.g. learning targets too) who will be interactive and activate one another, enabling complex transfer processes which can be turned into a model. Mathematically speaking this means that we will come across matrixes (Kommers, 1990; Vos, 1997). We shall not explore any further into this direction here.
A qualitative model (analogon) about how instruction and knowledge absorbtion work can be visualised by means of the model from figure 11 or 12 and reproduced 'dynamically'.
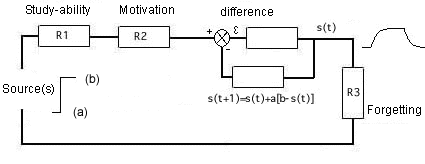
Figure 12. Study-ability is in this model in series with motivation. The higher the study-ability, i.e. the lower the resistance (R2), the better learning will proceed. The higher the motivation, i.e. the lower the resistance (R2) the better someone's absorption of useful things (knowledge, information, insight and possibly wisdom. And vice versa, the higher the resistance in R1 and R2 (in series) the worse learning will proceed. Simulation increases motivation for learning of about the same matter from books. R1 and R2 are in series and reinforce one another. This is the same in reality: study-ability and motivation should be added up. The replacement resistance for resistances in series equals R1+R2.
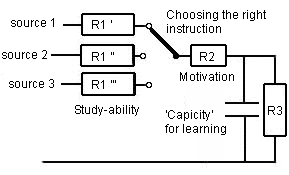
Figure 13. A large (and differentiated) supply of (learning tools). It has been indicated here that a student chooses the instruction tools or knowledge sources himself. There is an enormous supply. Resistance against the one (e.g. against study-ability) is higher or lower than against the other instruction (or learning tool).
The resistance which a teacher or instructor experiences in a pupil, is represented by resistance R2. The second resistance, R3 is the 'leakage resistance' over the condensator and it symbolises forgetting. We found an article in Dutch about this. This article by Meerling of the University of Leiden (1981) deals with a model (from 1880!) by Ebbinghaus and it strongly stresses 'forgetting' and not so much 'learning'. His model is therefore a 'quantitative' model (on an empirical basis) for forgetting rather than a 'qualitative' model for learning; let alone an analogon for learning. Ebbinghaus models the so-called 'forget curve' as pn=pl(1-a)^n-l, where pn represents the percentage of wrong responses; p1 prior knowledge and a intelligence for example. In our view the quantitative approach research has more or less come to a standstill. Apparently a more complete qualitative model should first be developed. His article suggests accuracy which in our opinion is not possible in this way. And certainly not at this stage of model formation about learning. However, the time for a qualitative model has come.
Discussion
We shall deal with three models in the discussion: (1) the learning models, (2) the model of learning here proposed, and (3) a new approach of design: the design model.
Learning-models: The learning models (LM) by Min (1997) have been developed in 1995 by Groenewoud& ter Burg (1996) already. Initially they were qualitative by nature. Now he is working to become them more quantitative.
Model for learning: Our model for learning is characterised by an integrating system. It is best to take the analogon as feedback integrator. It fits quite well and enables us to establish relation with motivation and study-ability. Something which we have always aimed to achieve. The model with the condensator, however fitting and simple, should be avoided in order to prevent unnecessary discussions.
Design models:
Figure 15 shows that design also knows something similar and therefore such a model can be established. A model, for learning describing the design cycle. An analogon for design. An educational solution always has (if all is well) a moment of 'measuring' (the evaluation) and a feedback loop which is followed so often until the measured value is equal to the desired value (b). A designer also wants a difference of zero
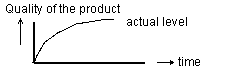
Figure 14. The quality level of a product increases in time as well. The OKT model has a feedback loop in which the evaluation (measuring) is the most important part. If you include an evaluation - however small and simple - you secure yourself against risks as in a system without a feedback like a feed forward system always has. Feed forward systems are quite useless in actuality when there are interruptions or setbacks. When the measured quality matches the desired quality the product or the solution are ok. (See literature about the 'theory of Quality Control' of Juran, 1962)
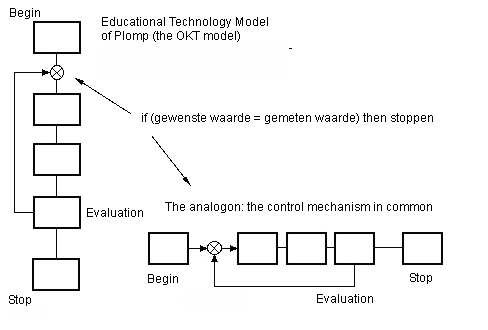
Figure 15a (on the left) and b (on the right). A similar control system. The OKT model also has in principle the same control circuit as our model. The designing proces has a dynamic similar to learning: accumulation of knowledge versus accumulation of the quality of a product (final target). If one turns the OKT model (left) one quarter turn it becomes a feedback system with a 'measuring moment' (the evaluation) and a feedback loop that is passed so often until the value measured is equal to the desired value (right). A designer (also) wants zero difference. The designer will continue to work on his product or solution until the desired result ('goal') is achieved. There e=o. Then the designer will stop.
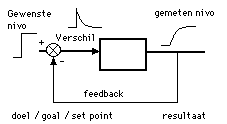
Figure 16. Designing as a feedback system.
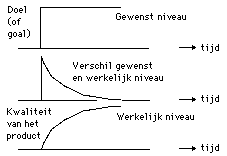
Figure 17. The three most important curves are: top: the 'target' that one has set at the beginning; middle: the difference between the desired value and the actual - measured - value. Below: the 'quality' of the product.
Further research should reveal whether this model, can offer a plausible explanation for a number of phenomena that are essential to understand in cohesion. It would also help solve the confusion about concepts, actors and effects.
Conclusions
This model will need a lot more polishing and it will have to be discussed extensively. The model on design is as yet unfinished. The 'learning models' have been investigated most often and are empirically based. The model can be tested online in our system 'LEARNING'. The influence of motivation and study-ability (of Wijnen) on 'learning' can be studied. We hope that this idea - and this model - will be of interest to others and that whoever is active in this field will contribute to the discussion.
Notes
Dr. ir. Rik Min and dr. ir. Hans Vos original are engineers; have their PhD and are both assistent professor at the University of Twente. Dr. Piet Kommers also has his PhD and is assistent professor at the University of Twente. Dr. Cor van Dijkum is assistent professor at the University of Utrecht, the Netherlands.
Address for correspondence: University of Twente, Faculty of Educational Science and Technology, P.O. Box 217, 7500 AE Enschede, the Netherlands. Phone: +31 -53.-489.3611, E-mail: min@edte.utente.nl, Web: http://users.edte.utwente.nl/min
Comments of colleagues: click here (grosslist, march, 2000).
References
Ashby, W.R. (1956)
An introduction to cybernetics; New York.
Atkinson, R.C. (1977)
Atkinson, R.L. (1977)
Atkinson, R.L., R.C. Atkinson, E.E. Smith, D.J. Bem and S. Nolen-Hoeksema (1996 12e editie) (2000 13th edition)
Introduction to psychology, Harcourt Brace Jovanovich, Forth Worth.
Anderson, R.C. (1977)
The notion of schemata and the educational enterprise; Schooling and the
aqusition of knowledge. pp. 415-432, Hillsdale, New Jersey: Lawrence Erlbaum
Associates.
Anderson, J.R. (1983)
The architecture of cognition; Cambridge, Massachusetts: Harvard University
Press.
Bush, R.R. & F. Mosteller (1955)
Stochastic model for learning. Wiley & Sons, Inc, New York; Chapman & Hall, Limited, London.
Ek, M., F. Gooters, C. v.d. Leest and J. Olde Achterweg (1995)
Quantitative and qualitative learning models in learning environments. (In Dutch) Internal paper. University of Twente
Ebbinghaus, H. (1992)
In: D. Ingleby & Spruijt. Ontdek de psychologie. Utrecht: Stichting Teleac; Utrecht: Lemma. (p. 110) (De vergeetcurve; 1885)
Gagne, R.M., (1965)
Conditions of learning; Holt, Rinehart & Winston, New York.
Groenewoud, U.A., J. ter Burg (1996)
Effect van mate van parallellisme op taakuitvoering en gepercipieerd gebruiksgemak. A internal research paper. University of Twente.
Hamaker, C. & V. Busato (2000)
Het geheugen; Amsterdam University Press. Amsterdam. ISBN 90-5356-431-4.
Juran (1962, first version)
Quality Control. MIT, Cambridge.
Kommers, P. A. M. (1990)
Hypertext and the acquisition of knowledge, PhD-thesis, University of Twente. ISBN 90-9003937-2.
Lave and March (1975)
Meerling (1981)
Min, F.B.M., (1999)
Interactive Micro-worlds on the World Wide Web. Int. J. of Continuing Engineering, Education and Long-life Learning, vol.9, no.2/3/4, p.302-314, ISSN 0957-4344. (Also published in concept on the web http://projects.edte.utwente.nl/pi/papers/JavaWeb.html)
Min, F.B.M. (1996)
Parallelism in working-, learning- and doing-environments; The Parallel Instruction Theory for Coaching in Open Learning Environments for Simulation; Proceedings of EuroMedia 96; Telematics in a multimedia environment, dec. 19-21, 1996; A publication of the Society for Computer Simulation International (SCS) (Eds. A. Verbraeck & P. Geril)
Min, F.B.M. (1995)
Simulation Technology & Parallelism in Learning Environments; Methods, Concepts, Models and Systems. Publisher: Academic Book Center, De Lier. ISBN 90-5478-036-3
Min, F.B.M. (1994)
Parallelism in open learning and working environments. British Journal of Educational Technology, Article; Vol. 25, No. 2, pp. 108-112. ISSN 0007-1013.
Min, F.B.M., (1992)
Parallel Instruction, a theory for Educational Computer Simulation. Interactive Learning Intern., Vol. 8, no. 3, 177-183.
Min, F.B.M., (1992)
Pilot-onderzoek naar 'leermodellen' bij computersimulatie aan de hand van observaties van leergedrag; Proceedings of 'Gezond onderwijscongres' on 28-29 november 1991 in Velthoven. Editors: C.P.M. van der Vleuten, A.J.J.A. Scherpenbier en M.C. Pollemans; Publisher: Bohn, Stafleu, Van Loghum BV. Houten. Pp. 130-137. ISBN 90-313-1489-7.
Min, F.B.M., H. Vos en P. Kommers (1998)
A model of learning. Lecture: Mai 26, 1998; University of Utrecht in Utrecht. On internet (in Dutch): http://projects.edte.utwente.nl/pi/papers/LerenModel.html (a paper).
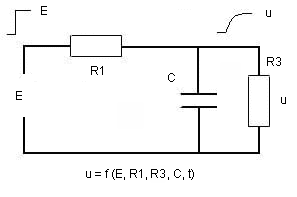
First type analogon of Min (first published for students in the course "systeembenadering in de onderwijskunde" by Vos and Min in 1997) (later by Min, F.B.M., H. Vos en P. Kommers, on internet in 1998): a resistance and a condensator as accumulator. The student has a certain capacity and wants to learn or to accumulate knowledge. Wanting to remember (and therefore learn) is represented by a condensator C; with a certain capacity for absorbtion (accumulation). U is supply: matter (from a book) or instruction (spoken by a teacher). Supply, instruction, matter are a 'voltage' source or a 'currency' source. Whichever. The transfer function here is of the type du/dt=1/RC (E-u) were R=R1. The instruction or instruction tool is assumed to be a voltage source (E) or currency source in our model. The point is here whether the student is susceptible for the instruction or not. Resistance R1 represents that resistance or reluctance. The reluctance to learn is usually strong. This also indicates that learning tools - such as simulations - begin at R1. Reluctance against instruction, reading, attending classes becomes less. After a few sessions with simulation programs the student is more susceptible to attending classes or instruction. (That is our thesis.) The 'demand for learning' has grown. The student is 'crying out' for information and/or instruction. He is more prepared 'to go to certain lengths' and read books about the subject of the simulation than before. R3 is the leakage resistance that represents forgetting.
Min, F.B.M., (1999)
A concept model about designing; an attempt to define accumulation processes as designing, controlling, learning & communication; On internet: http://projects.edte.utwente.nl/pi/papers/Designing.htm
(concept paper);
Parreren, C. F. van (1978) (6 th edition)
Psychologie van het Leren. Van Loghum Slaterus, Deventer.
Papert, S., (1980)
Mindstorms; Childeren, Computers and Powerful Ideas. Basic Books, Inc.,
Publishers; New York.
Richmond (1998)
Romiszowski, A.J., (1981)
Designing Instructional Systems. Kogan Page, London.
Spada, H. & W.F. Kempf (Eds.) (1977)
Structural Models of Thinking and Learning. Proceedings of the 7th IPN Symposium on Formalized Theories of Thinking and Learning and their implications for science Instruction. Hans Huber Publ., Vienna.
Vos, H. & Min, R, (1997)
Systeembenaderingen in de onderwijskunde ('System approach in Educational Science') (courses 1997/98) (in Dutch). Reader, University of Twente, Enschede.
Vos, H. (1997)
Methodenleer ('Methodology') (courses 1997/98) (in Dutch). Reader, University of Twente, Enschede.
Schmidt (1998)
personal announcement in discussion on the Nationale Onderwijs Research dagen
(Educational Research conference) in Enschede, the Netherlands (1998)
Enschede, 21 febr. 2000;
A. Updated an error R1 <-> R2 in sept. 13th 2001.
B. Interesting discussion about learning from Barry Kort
Subject: [IFETS-DISCUSSION:2626] Re: Strategic Control
To: ifets-discussion@catfish.valdosta.edu
Date: Tue, 18 Dec 2001 09:09:39 -0500 (EST)
Andrea Locke writes:
> As part of my research, I have a few questions about strategies used
to plan and control resources in organizations. I will greatly
appreciate any feedback, as it will be of much help to me in my
studies. Thank you all in advance for your input.
My first suggestion is to drop the word "control" in favor of "manage"
or "regulate".
> 1) In your corporation, or in general, how effective is corporate
governance with respect to strategic control?
Strategic Control is a pipe dream. The Desire for Control sets up
a conflict and a competition. It is a fundamental theorem of Control
Theory that one cannot control that which one cannot observe. And
so people in the organization devise clever and subversive ways to
prevent those in control from observing the parameters they seek to
regulate, thus derailing their ability to steer the helm.
> 2) How well does top management in your corporation use strategic
control to keep the company's internal dimensions aligned with its
external environment?
The external environment is one of relentless competition, undergirded
by subtle methods of fear induction, damage induction, pain induction,
and anguish induction (commonly known as "terrorism"). It is a mistake
for any organizization to align itself with that culture, as it's a
losing proposition. No sustainable system can emerge from a culture
driven by fear.
> 3) Does your company use competitive benchmarking standards (such
as PIMS) as a base for strategic control?
Never heard of PIMS.
Barry Kort, Ph.D.
MIT Media Lab
IFETS-DISCUSSION digest 339; wed 12/19/01 6:05 AM.



















