Een voorbeeld van een e-Learning-product met complexe applets

Met interactieve Java-applet(s)

Met interactieve JavaScript-animatie(s)

Met plaatjes, teksten en inklikregio's (rood)

Met parallelle instructie(s) over analoge schema's

Wat is een integrator?

In elk dynamisch model of regelsysteem zit altijd wel ergens een integrerend element of te wel een integrator. Daarom zullen we hier de begrippen integreren en integrator behandelen. Een integrator kan 'iets' integreren. Integreren is 'iets' accumuleren of optellen. Dat 'iets', dat aan de ingang staat, wordt steeds bij het reeds bestaande 'iets' dat er al in de integrator zit, opgeteld. Elke integrator heeft namelijk een startwaarde. Heel vaak is die startwaarde 0; maar ook heel vaak niet. Een integrator kan dat wat aan de ingang 'aangeboden' wordt, integreren. De snelheid van integreren hangt van parameters af.

Een visueel voorbeeld

De integrator is het beste te begrijpen door een voorbeeld. Hier wordt een waterbak als voorbeeld genomen. Zie figuur 1. Het is een bak waar water in en uit kan stromen. Dat in- en uitstromen gebeurt met twee pompjes. De pompjes zijn instelbaar. De hoeveelheid water in de bak is de variabele (de outputvariabele) ('V'). De flow door de pompjes in dit model zijn de parameters van het model. De waterhoogte hangt uiteindelijk van de hoeveelheid water en de vorm van de bak af en speelt in dit betoog - als eventuele tweede variabele - verder geen relevante rol meer; alleen visueel. De hoeveelheid water in het begin, op het tijdstip 0, is dan de startwaarde van de variabele. De bak is in het begin halfvol met water. De startwaarde van de hoeveelheid water, 'V', in de bak is hier dan dus 0.5 [liter].


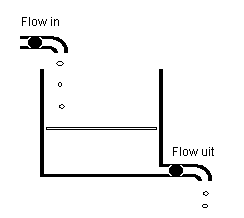
Figuur 1. Een bak met water en twee pompen. De ingaande stroom water is 'Flow in'; de uitgaande stroom is 'Flow uit'.

In figuur 1 is de bovenste pomp ingesteld op een flow met een bepaalde waarde en de onderste pomp op een andere waarde. Deze twee parameters plus de startwaarde bepalen gedurende de tijd dat het model loopt, de hoeveelheid water in de bak. De namen van de twee parameters zijn 'Flow in' en 'Flow uit'. Deze waarden zijn gedurende de proef of gedurende de simulatie in het algemeen tijdelijk constant. Bijvoorbeeld 2, resp. 1 [liter/min]. De eenheid van de twee parameters zijn beiden 'liter/min'; die van de enige outputvariable is 'liter'.


Figuur 2. Een screendump van de simulator. Je zult zo direct op deze site zelf kunnen zien hoe de variabele ten opzichte van de parameters omhoog of omlaag gaat.

In figuur 2 is een en ander bij elkaar gezet: een tekening van de waterbak en het symbool van de integrator, terwijl de outputvariabele 'level of the water' ('V') in blauw is aangegeven. 'Flow in', 'Flow uit' en 'V' zijn terug te vinden in het schema; rechts op de screendump van de simulator.

Complete schema's en losse symbolen

Van een wiskundig model, een proces of van een systeem kan een schema worden gemaakt. In schema's van processen, systemen of modellen worden voor het gemak (altijd) gestandaardiseerde symbolen gebruikt: driehoeken, blokken en/of circels en combinaties daarvan. Een integrator is symbolisch als in figuur 3b voor te stellen. Als dit soort symbolen als uit figuur 3 worden gebruikt, dan wordt een dergelijk schema een analoge schema genoemd (van het woord analogon). We zullen in de voorbeeld van de waterbak twee symbolen de revu laten passeren: het symbool van de integrator zelf en het symbool van een opteller.


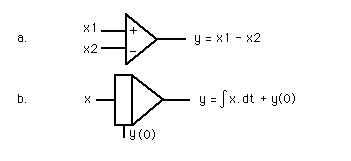
Een 'opteller' kan ingangswaarden of ingangssignalen bij elkaar optellen; of trekt ze van elkaar af. In het laatste geval dient er een 'min'-teken aan de ingang te staan. Er bestaan ook symbolen voor vermenigvuldigen en delen. Alleen de 'opteller', die ook 'negatief' of negatieve signalen kan optellen is - hier - voor ons relevant. (Zie figuur 3a.) De input c.q. het ingangssignaal bij een symbool als deze symbolen, is bijna altijd een variabele en bijna altijd van elders afkomstig.

In de regeltechniek wordt voor
een opteller of aftrekker
ook vaak en circel met een
maalteken erdoor gebruikt.
Zie hiernaast of figuur xxx en elders.
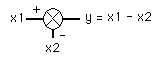Deze circel niet verwarren met
een ander symbool (met een cirkel) dat
een inputsignaal kan vermenigvuldigen
met een constante waarde.
Zie hiernaast of figuur xxx en elders.

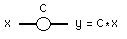Een 'integrator' telt steeds de waarde van de ingang (x) op bij de reeds aanwezige waarde (y). Het ingangswaarde kan positief of negatief zijn. Positief wil zeggen toenemende accumulatie; negatief wil zeggen minder of het omgekeerde van accumulatie ('negatieve accumulatie'). De formule die naast figuur 3b staat, spreekt voor zich.



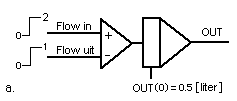
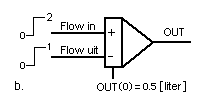
Het analoog schema van de waterbak met de twee pompen ziet er uit als in figuur 4 is afgebeeld. Figuur 4a is in alles - behalve visueel - uiteraard identiek aan figuur 4b. De input signalen zijn de waarden die de pompjes hebben.


Wat is een analoog schema
(Een korte tekst met uitleg - een instructie - die in een apart parallel window verschijnt; of in een boven- of onderliggend tab-blad)

Als er een constante waarde aan de ingang staat loopt de waarde van de output variabele lineair op (of af). Het verloop van de output bij dit proces, van de waterhoeveelheid in de waterbak, is meestal niet te voorspellen; die hangt af van de waarden die de de twee pompjes hebben en de momenten waarop de twee afzonderlijke pompjes (weer) een andere waarde krijgen.

In deze figuur 4 krijgt de parameter 'Flow in' op tijdstip t=0 oneindig lang de waarde 2 liter/min en 'Flow 2' oneindig lang de waarde 1 liter/min. Het zijn in feite constante input-variabelen ('constanten'). Je begrijpt dat de waterbak netto dan - constant - volloopt met 1 liter/min (2-1). De startwaarde is 0.5 liter. Dus na verloop van een minuut zit er 1.5 liter in de bak. Na twee minuten 2.5 liter.

Als de beiden pompjes nul zijn zal de hoeveelheid water niet toe- of afnemen. Als 'Flow uit' groter is dan 'Flow in' zal de bak snel leeg zijn. Test het zelf maar uit of beredeneer dit.

Dit voorbeeld van deze waterbak, het voorbeeld van een integrator, is een eerste orde proces. (Zie later; elders.) Er is hier geen enkele vorm van feedback.

Een animatie van de waterbak

Een animatie van deze waterbak met twee pompjes is in figuur 5 te zien. De animatie is dynamisch en interactief. Als de netto input van de integrator ('Flow in' minus 'Flow uit') groter is dan 0 dan wordt de output van de integrator groter dan de beginwaarde van de integrator (groter dan 0.5 liter). Als de netto input kleiner is dan 0 dan wordt de output kleiner. Een dergelijke waterbak werkt dus als een integrator.

Time: Height:

'Flow in' minus 'Flow uit', de netto input, is:
Naar links (netto instroom negatief) of naar rechts
(netto positief). Als de pomp netto op 0 staat stop de animatie.

Figuur 5. Een interactieve dynamisch animatie. Start de animatie
met klikken op 'Start the time' en door het naar links of rechts schuiven van de schuifbalk.

Dit soort animaties noemen we een 'model-driven' animatie. Het onderliggende wiskundige model van een integrator is gewoon een integraalvergelijking.

Een grafische simulatie van integreren

Naast een visuele interactieve animatie van de waterbak kun je ook eens naar een grafische interactieve simulatie van de waterbak kijken hoe integreren of accumuleren werkt. Eigenlijk heel eenvoudig. Zie figuur 6.

De grafische simulator is hier ook interactief. Je kunt de parameters 'Flow in' en 'Flow uit' veranderen en (anders) instellen. De variabelen die weergegeven worden in de tijd zijn de tijd (...) en de hoeveelheid water (...).

Figuur 6. Een interactieve dynamisch simulatie.
Dit is de output van de integrator grafisch gezien. Start deze simulator door op Continue te klikken en met de schuifjes de pompen in te stellen.

De hoeveelheid water in de bak is in het begin 0.5 [liter]. Er zijn twee interventiemogelijkheden: pomp 1 en pomp 2. Met deze pompjes kun je de flows regelen. In de simulatie is te zien dat als de tijd voortschrijd, de hoeveelheid water kan toenemen, afnemen of gelijk blijven. Als de beide pompen evenveel water per minuut pompen zal de netto flow gelijk blijven en de hoeveelheid water niet toe- of afnemen. Dit is ook het geval als gedurende de simulatie-run de beide flows nul zijn.

Het gedrag van een integrator te kennen en te begrijpen is heel belangrijk. Vooral in de tijd te zien en onder invloed van iets dat er 'in komt' en dat er 'uit kan gaan'.

Een voorbeeld met geld

De output van een integrator heeft een fysische dimensie. In het bovenstaande voorbeeld was dat water, maar het kan ook warmte of zelfs geld zelf. We geven je hier kort een voorbeeld met geld en zakgeld. Als je geen uitgaven doet en je heb geen inkomen, dan neemt de hoeveelheid geld in je portemonnee niet toe of af.

Gegeven is dat iemand 10 euro per week zakgeld krijgt. Gevraagd: wat is de hoeveelheid geld die je dan na een maand gespaard hebt?

De instroom is (dus) 10 euro per week. Dat is 'Flow in'. De 'Flow uit' is (hier) nul. Als je wel af en toe wat uitgeeft zal gedurende de tijd de hoeveelheid geld kleiner worden. Met dit model - van de integrator - kun je dus ook je uitgave-patroon simuleren en kijken of je geld overhoudt; en zo ja hoeveel.

Een tweede vraag is: wat gebeurt er in de tijd en hoe kunnen we dat grafisch weergeven? Je ziet dat er nog een belangrijk gegeven ontbreekt.

Je moet namelijk weten en dus nagaan hoeveel geld er al in zijn portemonnee zat of - wat ook kan - hoeveel er uiteindelijk in zijn portemonnee zit. De eerste waarde noemen we de startwaarde. De laatste waarde is de waarde die we willen voorspellen of waarmee je soms kunt terugrekenen.

Kijk naar figuur 7. Als je uitgaat dat deze persoon tijdstip t0 100 euro in zijn portemonnee heeft, dan heeft hij daar na één week 110, na twee weken 120 en na 4 weken 140 euro in. De voorspelde hoeveelheid geld is dan 140 [euro].


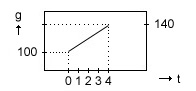
Figuur 7. De toename van geld ('g') in de tijd ('t'). De tijdseenheid is week. De geldeenheid is euro.

Bij een startwaarde van 100 op tijdstip t1=0 is dat in tabelvorm: 

tijd:         g:
 0 [week]    100 [euro]
 1           110
 2           120
 3           130
 4           140

We noemen de toename van de tijd per stap de stapgrootte; ook wel 'delta t' of 'dt'. De stapgrootte bij dit model is 1 [week]. De toename van g is per stapgrootte 10 [euro].

We hadden hier ook een voorbeeld kunnen nemen over warmte en een kachel. Als een kachel of een verwarming in een vertrek altijd blijven branden, en er geen feedback of termostaat is, stroomt er steeds een continue hoeveelheid warmte per uur dat vertrek binnen. De temperatuur stijgt niet onbeperkt omdat er in de praktijk altijd warmte weglekt door de ramen, de vloeren of het plafond. De temperatuur is echter te regelen. Dat gebeurt met een feedback 'aan te brengen'.

Wat doet feedback bij dit proces

Door feedback wordt een (gewoon) proces een (echt) systeem. Daarvoor is een termostaat nodig. De termostaat kan ingesteld worden op een gewenste waarde en vergelijkt de werkelijke waarde in het vertrek met de gewenste waarde die je hebt ingesteld. Een termostaat is een vergelijkend element en eigenlijk een 'opteller', maar dan met een + en een - signaal. Zie figuur 8. Je ziet wellicht al wat er dan zal gebeuren.


Figuur 8. De integrator met terugkoppeling. Tau is de tijdsconstante van dit systeem.

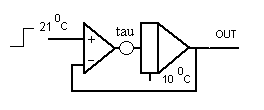
In figuur 8 is er 'over het proces' een 'terugkoppeling' aangebracht. Het proces is een domme warmtebron die een bepaalde hoeveelheid warmte per tijdseenheid geeft. Het gedrag van dit systeem - met de integrator als proces in het midden - is nu als volgt: Omdat de termostaat op 21 graden Celcius is gezet en het vertrek blijkbaar 10 graden Celcius is, is er een positief signaal aan de ingang van de integrator, zodanig dat er warmte wordt gemaakt. Als de hoeveelheid warmte zodanig is toegenomen dat de temperatuur in het vertrek 21 graden wordt, dan stopt de warmte accumulatie. Wordt de temperatuur door allerlei warmte-lekages lager dan 21 graden dan zal de warmte bron weer (even) aanslaan.

Maar zie daarvoor de andere lessen.


Dit interactieve product over 'integratoren' en 'analoge schema's' is in 2008 gemaakt voor ROC Hengelo. Het staat met andere lessen 'Regeltechiek' op de site van 'Acone Regeltechiek' en is daar voor ROC-studenten en publiek toegankelijk. Er zijn (daar) meerdere e-lessen, elders, m.n. over 'eerste orde en tweede orde regelsystemen'. De docent in wiens opdracht dit gemaakt is, had maar een klein budget tot zijn beschikking. Digitale producten als dit, met interactieve applets, zijn heel goedkoop te maken en kunnen eindeloos uitgebreid worden. Er worden standaard 'building-blocks' voor gebruikt: libraries met eenvoudige en complexe meervoudige te gebruiken en vanuit html of JavaScript aan te sturen Java-applicaties.

Rik Min, Enschede, 2008, update 2018