Systemen met teruggekoppeling
Introductie van de control theory in het vak psychologische ergonomie
|
terugkoppeling
|
|
feedback
|
|
meten is weten
|
|
systeem-dynamica
|
|
regelen
|
|
besturen
|
|
of constant houden
|
Rik Min
(vakgroep/afdeling: Educatieve Instrumentatietechnologie; ISM)
Centre for Telematics and Information Technology (CTIT)
Faculty of Educational Science and Technology (EDTE) (TO)
University of Twente (UT)
Achtergrond verhaal:
- 1. Stoommachine...
- 2. Centrale verwarming...
- 3. Voorraadbeheersingssysteem (in winkels)...
-
- 5. Als je op een meertje zeilt en je kijkt niet steeds naar een kerktoren...
- 6. Als je met je ogen dicht, geblindoekt door de woestijn loopt...
- 7. Als je nooit in de spiegel kijkt...
- 8. Als je nooit eens met iemand praat... (en nooit feedback krijgt)
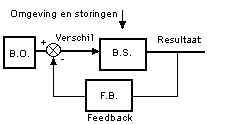
- De afzonderlijke onderdelen (blokken) van een systeem: het 'bestuurd systeem' (B.S.), de terugkoppellus (F.B.) en het 'besturend orgaan' (B.O.) (o.a. Kramer en De Smit, 1991).
- Duidelijk te zien is de feedback loop. Bij een geregeld systeem - een systeem dat kan vergelijken - is er altijd sprake van een (of meerdere) feedback-lussen.
- Een evaluatiemoment (van blok met + en -) is standaard en essentieel om de 'kwaliteit' van het 'product' (de output-variabele 'Resultaat') te kunnen bewaken.
- Zonder feedback-loop zou men nooit overeenstemming kunnen krijgen met een gewenste waarde.
- Dit systeem streeft er naar om het verschil zo klein mogelijk te houden.
- 1. het 'bestuurd(e) systeem' (B.S.)
- 2. het 'besturend orgaan' (B.O.)
- 3. de feedback lus
- 4. het vergelijkingselement om de 'kwaliteit' van het 'product' te kunnen bewaken (de 'comparator').
- 1e orde bestuurd systeem (B.S.)
- 2e orde bestuurd systeem (B.S.)
- 3e orde bestuurd systeem (B.S.)
- (nog) hogere orde bestuurd systeem (B.S.)
Voorbeelden: een fabriek, een auto, een zeilboot, een open haard, een verwarmingsketel, armen en benen (dus de losse processen zonder controle mechanisme en zonder feedback).
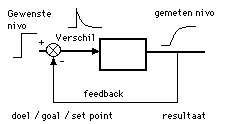
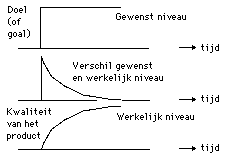
- Als je een doel stelt komt het systeem in aktie. Stel je doel is 10.
- Het verschil tussen de output (0) en de input (10) is dan maximaal 10. Het systeem 'gaat dan werken'.
- Het verschil tussen de output (5) en de input (10) wordt minder. Hier dan bijvoorbeeld 5. Het systeem gaat minder werken.
- Het verschil tussen de output (9) en de input (10) wordt nog minder. Hier dan nog maar 1. Het systeem gaat nog minder zijn best doen.
- Ten slotte: Het verschil tussen de output (10) en de input (10) is op een gegeven tijdstip 0 geworden. Het systeem doet dan niks meer. Dat is dan ook de steady state. Die situatie kan eindeloos voortduren.
- 1. het hongergevoel
- 2. de vochtbalans (veel drinken; weinig drinken)
- 3. leren (door het stellen van doelen, etc.)
-
- 5. de rol van de ogen (waarnemen) (het effect van een bril)
- 6. de rol van de hersens (vergelijken) (het effect van drugs)
- 7. de rol van armen en benen (uitvoering) (het effect van spierziekte)
- 8. de evenwichtsorganen (bij/in de oren)
-
- 10. de mens als black box: met ogen/oren (IN) en handen/voeten (OUT)
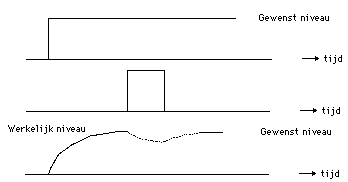
- Je ziet dat hier een systeem - op een gegeven moment - in een 'steady state' is gekomen.
- Als er (dan) (op een bepaald moment) een verstoring komt - naar boven of naar beneden - zie je dat het systeem zichzelf gaat bijregelen totdat de gewenste waarde (weer) wordt bereikt.
- Conclusie: het systeem is 'stabiel' en de output blijft (keurig) om het 'set point' schommelen...
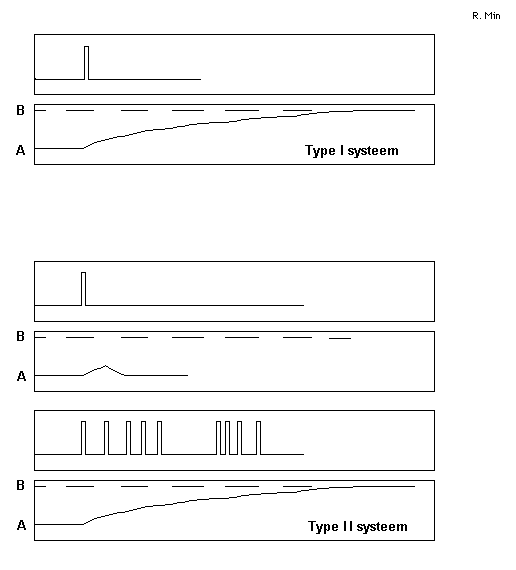
- U ziet een systeem dat direct reageert op een ingangssignaal: Type 1.
- U ziet daaronder een systeem waarbij het bijna niet mogelijk is dat het reageert op een ingangssignaal: type 2. Om echt een bepaald niveau te halen is een (enorme) inspanning nodig: Type 2.
- Voorbeelden: Type 1: roddels over Bill Clinton. Binnen de korste keren weet iedereen ze. Korte input: grote gevolgen. Type 2: naamsbekendheid van een nieuw merk. Daar zijn voortdurend advertentiecampagnes voor nodig. Korte input: minieme gevolgen
- Kun je een van de tijdconstanten van het bestuurde systeem eens twee maal groter maken ('tau1' of 'tau2'). Hoe lang doet het geregelde systeem er dan over om op de gewenste waarde te komen?
- Kun je de halfwaardetijd uitrekenen in het eerste demonstratievoorbeeld (figuur 3)? (Dat is de hoeveelheid tijd die het kost om de output op de helft van de maximale gewenste waarde te laten komen.)
- Kun je in het tweede demonstratievoorbeeld (figuur 4) de snelheid van het systeem eens zo groot mogelijk maken?
- Kun je in het derde demonstratievoorbeeld (figuur 5) een kortdurende 'positieve' storing aanbrengen. Wat zie je?
- Kun je in het derde demonstratievoorbeeld (figuur 5) een kortdurende 'negatieve' storing aanbrengen. Wat zie je?
- Wat is 'conditioning' in dit verband?
- Noem de belangrijkste 'controlled variable' bij een (gecontroleerde) stoommachine?
- Is de control theory een paradigma shift in de psychologie? Verklaar.
- Wat is (hier) de relatie tussen behavior and control? Verklaar.
- Waar zit het 1e en 2e orde verschil (in dit verband) in?
- Geef een goed voorbeeld van een systeem met een goed voorbeeld van een steady state.
- Zijn deterministische systemen nog wel (altijd) nuttig?
- Noem een paar goede voorbeelden van stimuli?
- Wat is een analogon? Noem er eens twee.
- Weet je wat - in dit verband - een dode tijd is?
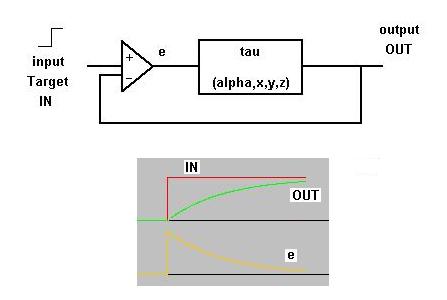
Figuur 6a. 1e orde proces met terugkoppeling.
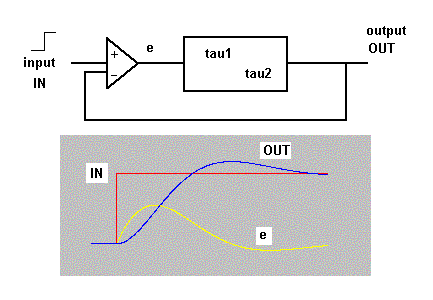
Figuur 6b. 2e orde proces met terugkoppeling.
- U ziet in figuur 6a de output en de input van een 1e orde systeem met terugkoppeling, incl. e, het verschil tussen OUT en IN. (Kenmerk: een tijdconstante genaamd 'tau'. Ander kenmerk: snelle start.)
- U ziet in figuur 6b de output en de input van een 2e orde systeem met terugkoppeling, incl. e, het verschil tussen OUT en IN. (Kenmerk: twee tijdconstanten genaamd 'tau1' en 'tau2'. Ander kenmerk: langzame start.)
- Tweede orde sytemen vertonen - onder bepaalde omstandigheden - zogenaamde overshuut reacties, dat wat eerste orde systemen niet kennen. Probeer het zelf maar. Zorg dat je en goede 'java-machine' op je PC hebt. Werken de aspplets niet: vraag er dan bij uw helpdesk naar.
- Het aantal tijdconstanten (van/in het B.S.-deel) bepaalt altijd heel sterk het 'overall gedrag' van het totale teruggekoppelde systeem (qua input-output-reactie).
- Autorijden als je drugs gebruikt hebt;
- De wetgevende macht (B.O.); de uitvoerdende macht (B.S.); de controlerende macht (de rechtbank) (in de vergelijkende rol);
- De wetgevende macht (regering en Tweede Kamer); de uitvoerdende macht (de ambtenaren, de bedrijven, de burger); de controlerende macht (de Tweede Kamer) (in de vergelijkende rol);
- xxxx
Enschede: mei/juni 2003. Versie 17:18, June, 6, 2003







