|
|
 |
In een kerstboom gaat de hele verlichting uit als je een van de lampjes uitdraait of als een van de lampjes stuk gaat. Dit gebeurt omdat
al de lampjes in zo'n verlichting in serie zijn geschakeld. Er bestaan ook lampjes die de keten niet verbreken. Op deze pagina zullen we verder toelichten hoe die lampjes werken.
We spreken van een serie schakeling als de stroom niet vertakt. Het kenmerk van een serie schakeling is dat de stroomsterkte (I) over alle apparaten dezelfde waarde
heeft. Voorbeeld 1: we sluiten twee weerstanden in serie aan op een batterij (z Als je nu R1 en R2
wilt vervangen met één weerstand, de zogenaamde 'vervangingsweerstand', dan moet je zorgen dat bij de vervanging de stroomsterkte niet verandert. De stroomsterkte is nu
0,12A bij een batterijspanning van 6,0V. Hieruit volgt dat RV een waarde van 6,0V / 0,12A = 50 heeft. Conclusie: Twee in serie geschakelde weerstanden kan je vervangen door een weerstand. Er
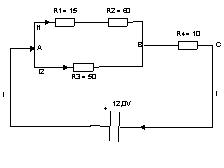
geldt dan de formule RV = R1 + R2. Voorbeeld 2: we sluiten een lampje en twee weerstanden in serie op 12V aan (zie figuur 6). Het la
De parallel schakeling
Bij een parallel schakeling zijn beide weerstanden op dezelfde bron aangesloten. De stroom van de bron wordt dan verdeeld over de weerstanden. Het kenmerk van een parallel schakeling is,
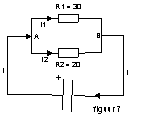
dat de spanning over elke weerstand gelijk is aan de spanning die er in de schakel is vlak voor de vertakking. Dus de spanning tussen de punten A en B in figuur 7. Voorbeeld 1: Stel dat er twee weerstanden R1 = 30 en R2 = 20
parallel geschakeld zijn en op een batterij van 6,0V zijn aangesloten (zie figuur 7). Voor de stroomsterkte I1 geldt dan: I1 = 6,0V / 30 = 0,20A.En voor de stroomsterkte I2 geldt: I2
= 6,0V / 20 = 0,30A. Ook de hoofdstroom kan nu berekent worden I = 0,20A + 0,30A = 0,50A. Hier kun je ook de twee weerstanden vervangen door RV. Omdat de stroom een waarde van I
= 0,5A bij een spanning van 6,0V, kunnen we de weerstandswaarde van RV berekenen. RV = 6,0V / 0,50A = 12. Hier geldt dus de formule 1/RV = 1/R1 + 1/R2
. Controleer maar: 1/RV = 1/30 + 1/20 = 5/60 RV = 12
Schakel je drie weerstanden van respectievelijk 10, 100 en 1000 in serie dan geldt RV = 1110, dit is groter dan 1000. Als je ze echter parallel schakelt, geldt RV = 9, dit is kleiner dan 10. naar de bovenkant van de pagina Serie en parallel gecombineerd
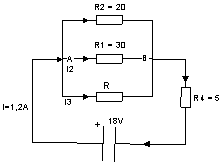
Veel schakelingen van weerstanden zijn 'gemengde' schakelingen. Serie en parallel komen dan gecombineerd voor. Voorbeeld 1: Bereken de stromen en de waarde van R.
We beginnen met de weerstand van 5 (R4), want daar heb je genoeg gegevens van: V4 = 1,2A · 5 = 6,0V (V = I · R).Voor de spanning tussen A en B blijft dan over: VAB = 18V 6V = 12 V (Vbat = V1 + V2) Pas twee keer de wet van Ohm toe (in een parallel schakeling blijft V constant):
Voorbeeld 2: Bereken de hoofdstroom (I) en de twee takstromen (I1 en I2 ).
Om te beginnen moet je de vervangingsweerstand berekenen: Nu kan de hoofdstroom (I) berekend worden:
Om de takstromen te berekenen moet je eerst weten hoe groot de spanning is die tussen de A en Bstaat. Dit kan op twee manieren:
De takstromen kunnen nu berekent worden: naar de bovenkant van de pagina
|
| [Inleiding] [Electriciteit thuis] [Wet van Ohm] [Schakelingen] [Transistor] |
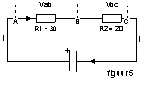 ie figuur 5). De weerstanden hebben respectievelijk de waarden R1=30 en R2=20. Stel dat de stroomsterkte 0,12A is. Dan staat er over R1 een spanning VAB
= (0,12A) · (30) = 3,6V.En over R2 staat een spanning VBC= (0,12A) · (20) = 2,4V.De spanning van de batterij kan je nu ook berekenen, want er geldt Vbat=VAB + VBC. Dus Vbat
= 3,6V + 2,4V = 6V.
ie figuur 5). De weerstanden hebben respectievelijk de waarden R1=30 en R2=20. Stel dat de stroomsterkte 0,12A is. Dan staat er over R1 een spanning VAB
= (0,12A) · (30) = 3,6V.En over R2 staat een spanning VBC= (0,12A) · (20) = 2,4V.De spanning van de batterij kan je nu ook berekenen, want er geldt Vbat=VAB + VBC. Dus Vbat
= 3,6V + 2,4V = 6V.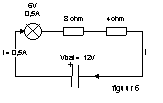 mpje brandt goed op 6V bij 0,5A. Dat is nu ook het geval. De stroomsterkte door de
weerstanden is dus ook 0,5A. Met de wet van ohm en de kennis uit het vorige voorbeeld kunnen we nu de spanning over de weerstanden uitrekenen. Over R1 staat 4V (0,5A · 8) en over R2
staat 2V (0,5A · 4). Als het lampje in de keten stuk is, zit er een gat in de keten. Het gevolg hiervan is dat er nergens stroom loopt. Er staat dan 12V over het gat en 0V over de weerstanden.
mpje brandt goed op 6V bij 0,5A. Dat is nu ook het geval. De stroomsterkte door de
weerstanden is dus ook 0,5A. Met de wet van ohm en de kennis uit het vorige voorbeeld kunnen we nu de spanning over de weerstanden uitrekenen. Over R1 staat 4V (0,5A · 8) en over R2
staat 2V (0,5A · 4). Als het lampje in de keten stuk is, zit er een gat in de keten. Het gevolg hiervan is dat er nergens stroom loopt. Er staat dan 12V over het gat en 0V over de weerstanden.